Distribución de Poisson.
= El eje horizontal es el índice x. La función solamente está definida en valores enteros de k. Las líneas que conectan los puntos son solo guías visuales y no indican continuidad. Función de densidad de probabilidad
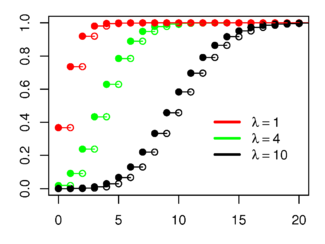= El eje horizontal es el índice k. Función de distribución de probabilidad
Parámetros	${\displaystyle \lambda \in (0,\infty )}$
Dominio	${\displaystyle k\in \{0,1,2,\ldots \}}$
Función de probabilidad (fp)	${\displaystyle {\frac {e^{-\lambda }\lambda ^{k}}{k!}}\!}$
Función de distribución (cdf)	${\displaystyle {\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}}\!{\text{ para }}k\geq 0}$ (donde Γ(x, y) es la función gamma incompleta)
Media	${\displaystyle \lambda \,}$
Mediana	${\displaystyle {\text{usualmente cerca de }}\lfloor \lambda +1/3-0.02/\lambda \rfloor }$
Moda	${\displaystyle \left\lceil \lambda \right\rceil -1}$
Varianza	${\displaystyle \lambda \,}$
Coeficiente de simetría	${\displaystyle \lambda ^{-1/2}\,}$
Curtosis	${\displaystyle 3+\lambda ^{-1}\,}$
Entropía	${\displaystyle \lambda [1\!-\!\ln(\lambda )]\!+\!e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\ln(k!)}{k!}}}$
Función generadora de momentos (mgf)	${\displaystyle \exp(\lambda (e^{t}-1))\,}$
Función característica	${\displaystyle \exp(\lambda (e^{it}-1))\,}$
[editar datos en Wikidata]

En teoría de probabilidad y estadística, la distribución de Poisson es una distribución de probabilidad discreta que expresa, a partir de una frecuencia de ocurrencia media, la probabilidad de que ocurra un determinado número de eventos durante cierto período de tiempo. Concretamente, se especializa en la probabilidad de ocurrencia de sucesos con probabilidades muy pequeñas, o sucesos «raros». También puede utilizarse para contar el número de eventos o partículas consideradas puntuales en otros tipos de intervalos específicos, como la distancia, el área o el volumen.

Fue propuesta por Siméon-Denis Poisson, que la dio a conocer en 1838 en su trabajo Recherches sur la probabilité des jugements en matières criminelles et matière civile (Investigación sobre la probabilidad de los juicios en materias criminales y civiles).

Por ejemplo, un centro de llamadas recibe una media de 180 llamadas por hora, 24 horas al día. Las llamadas son independientes; recibir una no cambia la probabilidad de que llegue la siguiente. El número de llamadas recibidas durante cualquier minuto tiene una distribución de probabilidad de Poisson con media 3: los números más probables son 2 y 3, pero 1 y 4 también son probables y hay una pequeña probabilidad de que sea tan bajo como cero y una probabilidad muy pequeña de que pueda ser 10.

Otro ejemplo es el número de desintegraciones que se producen en una fuente radiactiva durante un periodo de observación determinado.

La distribución fue introducida por primera vez por Siméon Denis Poisson (1781-1840) y publicada junto con su teoría de la probabilidad en su obra Recherches sur la probabilité des jugements en matière criminelle et en matière civile (1837).^[1]​ El trabajo teorizaba sobre el número de condenas injustas en un país determinado centrándose en ciertas variables aleatorias N que cuentan, entre otras cosas, el número de sucesos discretos (a veces llamados "eventos" o "llegadas") que tienen lugar durante un intervalo de tiempo-intervalo de duración determinada. El resultado ya había sido dado en 1711 por Abraham de Moivre en De Mensura Sortis seu; de Probabilitate Eventuum in Ludis a Casu Fortuito Pendentibus .^[2]​^[3]​ ^[4]​^[5]​. Esto la convierte en un ejemplo de ley de Stigler y ha llevado a algunos autores a defender que la distribución de Poisson debería llevar el nombre de Moivre.^[6]​

En 1860, Simon Newcomb ajustó la distribución de Poisson al número de estrellas encontradas en una unidad de espacio.^[7]​ Otra aplicación práctica de esta distribución fue realizada por Ladislaus Bortkiewicz en 1898, cuando se le encomendó la tarea de investigar el número de soldados del ejército prusiano muertos accidentalmente por patadas de caballos;^[8]​ este experimento introdujo la distribución de Poisson en el campo de la ingeniería de la fiabilidad.

La distribución de Poisson es popular porque modela el número de veces que ocurre un evento en un intervalo de tiempo.

Sea ${\displaystyle \lambda >0}$ y ${\displaystyle X}$ una variable aleatoria discreta, si la variable aleatoria ${\displaystyle X}$ tiene una distribución de Poisson con parámetro ${\displaystyle \lambda }$ entonces escribiremos ${\displaystyle X\sim \operatorname {Poisson} (\lambda )}$ o ${\displaystyle X\sim \operatorname {Poi} (\lambda )}$.

Una variable aleatoria discreta X se dice que tiene una distribución de Poisson, con parámetro ${\displaystyle \lambda >0,}$ si tiene una función de probabilidad dada por:^[9]​^: 60

${\displaystyle f(k;\lambda )=\operatorname {P} (X{=}k)={\frac {\lambda ^{k}e^{-\lambda }}{k!}},}$

donde

• k es el número de ocasiones (${\displaystyle k=0,1,2,\ldots }$)
• e es número de Euler (${\displaystyle e=2,71828\ldots }$)
• ! es la función factorial.

La distribución de Poisson puede ser útil para modelizar sucesos como:

• El número de meteoritos de más de 1 metro de diámetro que chocan contra la Tierra en un año;
• el número de fotones láser que chocan contra un detector en un intervalo de tiempo determinado; y
• el número de estudiantes que obtienen una nota baja y una nota alta en un examen.

La distribución de Poisson es un modelo apropiado si se cumplen los siguientes supuestos:^[10]​

• k es el número de veces que ocurre un suceso en un intervalo y k puede tomar los valores 0, 1, 2, ... .
• La ocurrencia de un suceso no afecta a la probabilidad de que ocurra un segundo suceso. Es decir, los sucesos ocurren de forma independiente.
• La tasa media a la que se producen los sucesos es independiente de cualquier suceso. Para simplificar, se suele suponer que es constante, pero en la práctica puede variar con el tiempo.
• Dos sucesos no pueden ocurrir exactamente en el mismo instante; en cambio, en cada subintervalo muy pequeño, o bien ocurre exactamente un suceso, o no ocurre ningún suceso.

Si estas condiciones son ciertas, entonces k es una variable aleatoria de Poisson, y la distribución de k es una distribución de Poisson.

La distribución de Poisson es también el límite de una distribución binomial, para la cual la probabilidad de éxito de cada ensayo es igual a λ dividida por el número de ensayos, a medida que el número de ensayos se aproxima a infinito (véase Distribuciones relacionadas).

Si ${\displaystyle X\sim \operatorname {Poisson} (\lambda )}$ entonces la función de probabilidad es

${\displaystyle \operatorname {P} [X=k]={\frac {e^{-\lambda }\lambda ^{k}}{k!}}}$

donde ${\displaystyle k=0,1,2,\dots }$ es el número de ocurrencias del evento o fenómeno.

El parámetro ${\displaystyle \lambda >0}$ representa el número de veces que se espera que ocurra dicho fenómeno durante un intervalo dado. Por ejemplo, si el suceso estudiado tiene lugar en promedio 4 veces por minuto y estamos interesados en la probabilidad de que ocurra ${\displaystyle k}$ veces dentro de un intervalo de 10 minutos, usaremos un modelo de distribución de Poisson con λ = 10×4 = 40.

En ocasiones, para calcular las probabilidades, se utiliza la siguiente fórmula recursiva para calcular ${\displaystyle \operatorname {P} [X=k+1]}$ en términos de ${\displaystyle \operatorname {P} [X=k]}$

${\displaystyle {\begin{aligned}{\frac {\operatorname {P} [X=k+1]}{\operatorname {P} [X=k]}}&={\frac {\frac {e^{-\lambda }\lambda ^{k+1}}{(k+1)!}}{\frac {e^{-\lambda }\lambda ^{k}}{k!}}}\\&={\frac {\lambda ^{k+1}k!}{\lambda ^{k}(k+1)!}}\\&={\frac {\lambda }{k+1}}\end{aligned}}}$

por lo tanto

${\displaystyle \operatorname {P} [X=k+1]={\frac {\lambda }{k+1}}\operatorname {P} [X=k]}$

siempre que ${\displaystyle \operatorname {P} [X=k]\neq 0}$.

Si ${\displaystyle X\sim \operatorname {Poisson} (\lambda )}$ entonces la variable aleatoria ${\displaystyle X}$ satisface algunas propiedades.

La media de la variable aleatoria ${\displaystyle X}$ es

${\displaystyle \operatorname {E} [X]=\lambda }$

Esta se demuestra por definición de esperanza matemática

${\displaystyle {\begin{aligned}\operatorname {E} [X]&=\sum _{k=0}^{\infty }k\left({\frac {e^{-\lambda }\lambda ^{k}}{k!}}\right)\\&=e^{-\lambda }\sum _{k=1}^{\infty }{\frac {k\lambda ^{k}}{k!}}\\&=e^{-\lambda }\sum _{k=1}^{\infty }{\frac {\lambda ^{k}}{(k-1)!}}\\&=\lambda e^{-\lambda }\sum _{k=1}^{\infty }{\frac {\lambda ^{k-1}}{(k-1)!}}\\&=\lambda e^{-\lambda }\sum _{j=0}^{\infty }{\frac {\lambda ^{j}}{j!}}\\&=\lambda e^{-\lambda }e^{\lambda }\\&=\lambda \end{aligned}}}$

La varianza de la variable aleatoria ${\displaystyle X}$ es

${\displaystyle \operatorname {Var} (X)=\lambda }$

Demostración

Tenemos que ${\displaystyle \operatorname {Var} [X]=\operatorname {E} [X^{2}]-\operatorname {E} [X]^{2}=\operatorname {E} [X(X-1)+X]-\operatorname {E} [X]^{2}{\overset {\text{linealidad}}{=}}\operatorname {E} [X(X-1)]+\operatorname {E} [X]-\operatorname {E} [X]^{2}}$. Como ${\displaystyle E[X(X-1)]=\sum _{x\geq 0}^{}{x(x-1)P[X=x]}=\sum _{x\geq 2}^{}{x(x-1)e^{-\lambda }{\frac {\lambda ^{x}}{x!}}}=\sum _{x\geq 2}^{}{e^{-\lambda }{\frac {\lambda ^{x}}{(x-2)!}}}=\lambda ^{2}e^{-\lambda }\sum _{x\geq 2}^{}{\frac {\lambda ^{x-2}}{(x-2)!}}{\overset {y:=x-2}{=}}}$ ${\displaystyle =\lambda ^{2}e^{-\lambda }\sum _{y\geq 0}^{}{\frac {\lambda ^{y}}{(y)!}}{\overset {\text{Serie de Taylor}}{=}}\lambda ^{2}e^{-\lambda }e^{\lambda }=\lambda ^{2},}$ obtenemos que ${\displaystyle \operatorname {Var} [X]=\operatorname {E} [X(X-1)]+\operatorname {E} [X]-\operatorname {E} [X]^{2}=\lambda ^{2}+\lambda -\lambda ^{2}=\lambda \quad \square }$

Es decir, tanto el valor esperado como la varianza de una variable aleatoria con distribución de Poisson son iguales a ${\displaystyle \lambda }$.

Los momentos de orden superior son polinomios de Touchard en ${\displaystyle \lambda }$ cuyos coeficientes tienen una interpretación combinatoria. De hecho, cuando el valor esperado de la distribución de Poisson es 1, entonces según la fórmula de Dobinski, el ${\displaystyle n}$-ésimo momento iguala al número de particiones de tamaño ${\displaystyle n}$.

La moda de la variable aleatoria ${\displaystyle X}$ es

${\displaystyle \lfloor \lambda \rfloor }$

esto es, el mayor de los enteros menores que ${\displaystyle \lambda }$ (los símbolos ${\displaystyle \scriptstyle \lfloor \ \rfloor }$ representan la función parte entera).

La función generadora de momentos de la distribución de Poisson está dada por

${\displaystyle M_{X}(t)=\mathrm {E} \left[e^{tX}\right]=\sum _{x=0}^{\infty }e^{tx}\operatorname {P} [X=x]=\sum _{x=0}^{\infty }e^{tx}{e^{-\lambda }\lambda ^{x} \over x!}=e^{-\lambda }\sum _{x=0}^{\infty }{\frac {(\lambda e^{t})^{x}}{x!}}=e^{-\lambda }e^{\lambda e^{t}}=e^{\lambda (e^{t}-1)}.}$

Las variables aleatorias de Poisson tienen la propiedad de ser infinitamente divisibles.

La divergencia Kullback-Leibler desde una variable aleatoria de Poisson de parámetro ${\displaystyle \lambda _{0}}$ a otra de parámetro ${\displaystyle \lambda }$ es

${\displaystyle D_{\mathrm {KL} }(\lambda ||\lambda _{0})=\lambda \left(1-{\frac {\lambda _{0}}{\lambda }}+{\frac {\lambda _{0}}{\lambda }}\log {\frac {\lambda _{0}}{\lambda }}\right).}$

Un criterio fácil y rápido para calcular un intervalo de confianza aproximada de ${\displaystyle \lambda }$ es propuesto por Guerriero (2012).^[11]​ Dada una serie de eventos k (al menos el 15-20) en un periodo de tiempo T, los límites del intervalo de confianza para la frecuencia vienen dadas por:

${\displaystyle F_{low}=\left(1-{\frac {1.96}{\sqrt {k-1}}}\right){\frac {k}{T}}}$

${\displaystyle F_{upp}=\left(1+{\frac {1.96}{\sqrt {k-1}}}\right){\frac {k}{T}}}$

entonces los límites del parámetro ${\displaystyle \lambda }$ están dadas por:${\displaystyle \lambda _{low}=F_{low}T;\lambda _{upp}=F_{upp}T}$.

La suma de variables aleatorias de Poisson independientes es otra variable aleatoria de Poisson cuyo parámetro es la suma de los parámetros de las originales. Dicho de otra manera, si

${\displaystyle X_{i}\sim \mathrm {Poisson} (\lambda _{i})\,,i=1,\dots ,N}$

son N variables aleatorias de Poisson independientes, entonces

${\displaystyle Y=\sum _{i=1}^{N}X_{i}\sim \mathrm {Poisson} \left(\sum _{i=1}^{N}\lambda _{i}\right)\,}$.

La distribución de Poisson es el caso límite de la distribución binomial. De hecho, si los parámetros n y ${\displaystyle \theta }$ de una distribución binomial tienden a infinito (en el caso de n) y a cero (en el caso de ${\displaystyle \theta }$) de manera que ${\displaystyle \lambda =n\theta }$ se mantenga constante, la distribución límite obtenida es de Poisson.

Como consecuencia del teorema central del límite, para valores grandes de ${\displaystyle \lambda }$, una variable aleatoria de Poisson X puede aproximarse por otra normal dado que el cociente

${\displaystyle Y={\frac {X-\lambda }{\sqrt {\lambda }}}}$

converge a una distribución normal de media 0 y varianza 1.

Supóngase que para cada valor t > 0, que representa el tiempo, el número de sucesos de cierto fenómeno aleatorio sigue una distribución de Poisson de parámetro λt. Entonces, los tiempos transcurridos entre dos sucesos sucesivos sigue la distribución exponencial.

Si el ${\displaystyle 2\%}$ de los libros encuadernados en cierto taller tienen encuadernación defectuosa, para obtener la probabilidad de que ${\displaystyle 5}$ de ${\displaystyle 400}$ libros encuadernados en este taller tengan encuadernaciones defectuosas usamos la distribución de Poisson, si se define ${\displaystyle X}$ como el número de libros que tengan encuadernación defectuosa entonces ${\displaystyle k=5}$ y ${\displaystyle \lambda }$ (el valor esperado de libros defectuosos) es el ${\displaystyle 2\%}$ de ${\displaystyle 400}$, es decir, ${\displaystyle 8}$. Por lo tanto, la probabilidad buscada es:

${\displaystyle \operatorname {P} [X=5]={\frac {8^{5}e^{-8}}{5!}}=0.092}$

La distribución de Poisson se aplica a varios fenómenos discretos de la naturaleza (esto es, aquellos fenómenos que ocurren 0, 1, 2, 3,etc. veces durante un periodo definido de tiempo o en un área determinada y con un número definido de grados de libertad) cuando la probabilidad de ocurrencia del fenómeno es constante en el tiempo o el espacio. Ejemplos de estos eventos que pueden ser modelados por la distribución de Poisson incluyen:

• El número de autos que pasan a través de un cierto punto en una ruta (suficientemente distantes de los semáforos) durante un periodo definido de tiempo.
• El número de errores de ortografía que uno comete al escribir una única página.
• El número de llamadas telefónicas en una central telefónica por minuto.
• El número de servidores web accedidos por minuto.
• El número de animales muertos encontrados por unidad de longitud de ruta.
• El número de mutaciones de determinada cadena de ADN después de cierta cantidad de radiación.
• El número de núcleos atómicos inestables que se han desintegrado en un determinado período.
• El número de estrellas en un determinado volumen de espacio.
• La distribución de receptores visuales en la retina del ojo humano.
• La inventiva^[12]​ de un inventor a lo largo de su carrera.

• Distribución de Poisson Puntual
• Distribución de Poisson Acumulada
• Calculadora Distribución de Poisson
• Cálculo de la probabilidad de una distribución de Poisson usando R

• Ahrens, Joachim H.; Dieter, Ulrich (1974). «Computer Methods for Sampling from Gamma, Beta, Poisson and Binomial Distributions». Computing 12 (3): 223-246. S2CID 37484126. doi:10.1007/BF02293108. 
• Ahrens, Joachim H.; Dieter, Ulrich (1982). «Computer Generation of Poisson Deviates». ACM Transactions on Mathematical Software 8 (2): 163-179. S2CID 12410131. doi:10.1145/355993.355997. 
• Evans, Ronald J.; Boersma, J.; Blachman, N. M.; Jagers, A. A. (1988). «The Entropy of a Poisson Distribution: Problem 87-6». SIAM Review 30 (2): 314-317. doi:10.1137/1030059. 

• Proceso de Poisson
• Regresión de Poisson