En las redes neuronales artificiales, la atención es una técnica que pretende imitar la atención cognitiva. Este efecto realza algunas partes de los datos de entrada mientras que disminuye otras. La motivación es que la red debe dedicar más atención a las partes importantes de los datos, aunque puedan ser una pequeña porción de una imagen o una frase. El aprendizaje de qué parte de los datos es más importante que otra depende del contexto, y se entrena mediante descenso del gradiente.

Los mecanismos similares a la atención se introdujeron en los años 90 con nombres como módulos multiplicativos, unidades sigma pi,^[1]​ e hiperredes[.^[2]​ La flexibilidad de estos modelos proviene de la introducción de pesos "blandos" que pueden cambiar durante el tiempo de ejecución, en contraste con los pesos estándar que deben permanecer fijos en tiempo de ejecución. Entre los usos de la atención se incluyen la memoria en controladores de pesos rápidos,^[3]​ máquinas de Turing neuronales, tareas de razonamiento en ordenadores neuronales diferenciables,^[4]​ procesamiento del lenguaje en transformadores y LSTM, y procesamiento de datos multisensoriales (sonido, imágenes, vídeo y texto) en perceptores.^[5]​^[6]​^[7]​^[8]​

Correlacionar las distintas partes de una frase o una imagen puede contribuir a captar su estructura. El esquema de atención brinda una oportunidad a la red neuronal para lograrlo. Por ejemplo, en la frase "See that girl run." (en español: Mira a esa chica correr), cuando la red procesa "that" (en español: esa) queremos que sepa que esa palabra se refiere a "girl" (en español: chica). El siguiente diagrama muestra cómo una red correctamente entrenada puede conseguirlo.

Esquema de autoatención utilizado en el entrenamiento no supervisado de un modelo de lenguaje (Esquema nº 4 de la sección Variantes, que aparece abajo). La frase de entrada se divide en 3 vías de procesamiento (izquierda) y se fusiona al final en el vector Context (derecha), que puede ser alimentado a otra capa neuronal para predecir la siguiente palabra o hacer otras tareas. Para facilitar la notación, tomamos un tamaño de incrustación de palabras de 300 y un número de neuronas de 100 en cada subred de la cabeza de atención. - X es la matriz de entrada de incrustaciones de palabras, de tamaño 4 x 300. x es el vector de palabras para "that" (en español: esa). - La cabeza de atención consta de 3 redes neuronales a entrenar. Cada una tiene 100 neuronas con una matriz de pesos de tamaño 300 x 100. - (*) este cálculo es softmax( qKT / sqrt(100) ), sin V. Reescalando por sqrt(100) evita una gran variación en qKT que permitiría que una sola palabra dominara excesivamente el softmax, lo que daría lugar a que sólo se prestara atención a una palabra, como haría un hard max discreto. Notación: En este caso, la fórmula softmax por filas comúnmente escrita asume que los vectores son filas, lo que contradice la notación matemática estándar de vectores columna. Lo más correcto sería tomar la transposición del vector contextual y utilizar la fórmula softmax por columnas, lo que daría como resultado la forma más correcta. Context = (XVW)T * softmax( (KW XT) * (xQw)T / sqrt(100) ).

La estructura de los datos de entrada se captura en las ponderaciones Qw y Kw, y las ponderaciones Vw expresan esa estructura en términos de características más significativas para la tarea para la que se está entrenando. Por este motivo, los componentes de la cabeza de atención se denominan Query (Q), Key (K) y Value (V), una analogía poco precisa y posiblemente engañosa con los sistemas de bases de datos relacionales.

Podemos acelerar enormemente los cálculos paralelizando lo anterior. Tenga en cuenta que el vector de contexto de "that" no depende de los vectores de contexto de las demás palabras; por tanto, podemos calcular todos los vectores de contexto a la vez utilizando simplemente la matriz X de word embedding apiladas en lugar de x en la fórmula anterior. Ahora, el softmax debe interpretarse como un softmax matricial que actúa sobre filas separadas. Esto supone una enorme ventaja sobre las redes recurrentes, que deben operar secuencialmente.

Para construir una máquina que traduzca del inglés al francés, se injerta una unidad de atención en el codificador-decodificador básico (diagrama de abajo). En el caso más sencillo, la unidad de atención consiste en productos de puntos de los estados recurrentes del codificador y no necesita entrenamiento. En la práctica, la unidad de atención consta de 3 capas de red neuronal entrenadas y totalmente conectadas denominadas query (consulta), key (clave) y value (valor).

Codificador-decodificador con atención. La parte izquierda (líneas negras) es el codificador-decodificador, la parte central (líneas naranjas) es la unidad de atención y la parte derecha (en gris y colores) son los datos calculados. Las regiones grises de la matriz H y el vector w son valores cero. Los subíndices numéricos indican el tamaño de los vectores, mientras que los subíndices i e i - 1 indican los pasos temporales.

Vistos como una matriz, los pesos de atención muestran cómo la red ajusta su enfoque según el contexto.

Esta visión de los pesos de atención aborda el problema de la "explicabilidad" de las redes neuronales. Las redes que realizan traducciones literales sin tener en cuenta el orden de las palabras mostrarían las puntuaciones más altas a lo largo de la diagonal (dominante) de la matriz. La dominancia fuera de la diagonal muestra que el mecanismo de atención es más sofisticado. En la primera pasada por el descodificador, el 94% del peso de la atención recae en la primera palabra inglesa "I", por lo que la red ofrece la palabra "je". En la segunda pasada por el descodificador, el 88% del peso de la atención está en la tercera palabra inglesa "you", por lo que ofrece "t'". En la última pasada, el 95% de la atención se centra en la segunda palabra inglesa "love", por lo que ofrece "aime".

Muchas variantes de la atención aplican pesos suaves, como por ejemplo

• "focos internos de atención"^[10]​ generados por programadores de pesos rápidos o controladores de pesos rápidos (1992)^[3]​ (también conocidos como transformadores con "autoatención linealizada"^[11]​^[12]​). Una red neuronal lenta aprende por descenso de gradiente a programar los pesos rápidos de otra red neuronal a través de productos externos de patrones de activación autogenerados llamados "FROM" y "TO" ("DESDE" y "HACIA") que en terminología de transformadores se denominan "key" y "value". Este "mapeo de atención" de pesos rápidos se aplica a las queries (consultas).
• Atención de Bahdanau,^[13]​ también denominada atención aditiva,
• Atención de Luong^[14]​ que se conoce como atención multiplicativa, construida sobre la atención aditiva,
• autoatención altamente paralelizable introducida en 2016 como atención descomponible^[15]​ y utilizada con éxito en transformadores un año después.

Para las redes neuronales convolucionales, los mecanismos de atención pueden distinguirse por la dimensión sobre la que operan, en concreto: atención espacial,^[16]​ atención de canal,^[17]​ o combinaciones.^[18]​^[19]​

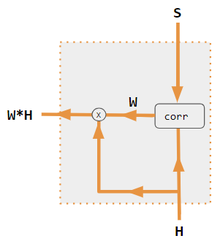
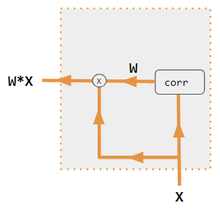
Estas variantes recombinan las entradas del lado del codificador para redistribuir esos efectos a cada salida objetivo. A menudo, una matriz de productos de puntos de tipo correlación proporciona los coeficientes de reponderación.

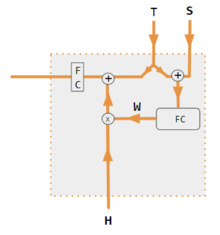
1. producto por puntos codificador-decodificador	2. QKV codificador-decodificador	3. producto por puntos sólo codificador	4. QKV sólo codificador	5. Tutorial de Pytorch

• Aprendizaje activo
• Alucinación (inteligencia artificial)
• Transformador de visión
• Transformador (modelo de aprendizaje automático), Atención escalada del producto escalar.

1. ↑ Rumelhart, David E.; Mcclelland, James L.; Group, PDP Research (29 de julio de 1987). «Chapter 2». Parallel Distributed Processing, Volume 1: Explorations in the Microstructure of Cognition: Foundations (en inglés) 1. Cambridge, Mass: Bradford Books. ISBN 978-0-262-68053-0. 
2. ↑ Yann Lecun (2020). Deep Learning course at NYU, Spring 2020, video lecture Week 6. Consultado el 8 de marzo de 2022. «Los eventos ocurren en 53:00». 
3. ↑ ^{a b} Schmidhuber, Jürgen. «Learning to control fast-weight memories: an alternative to recurrent nets». Neural Computation 4 (1): 131-139. doi:10.1162/neco.1992.4.1.131. 
4. ↑ Graves, Alex; Wayne, Greg; Reynolds, Malcolm; Harley, Tim; Danihelka, Ivo; Grabska-Barwińska, Agnieszka; Colmenarejo, Sergio Gómez; Grefenstette, Edward et al. (12 de octubre de 2016). «Hybrid computing using a neural network with dynamic external memory». Nature 538 (7626): 471 - 476. ISSN 1476-4687. PMID 27732574. doi:10.1038/nature20101.  Se sugiere usar |número-autores= (ayuda)
5. ↑ Vaswani; Parmar; Uszkoreit; Jones; Gomez; Kaiser; Polosukhin (2017-12-05). «Attention Is All You Need». arXiv:1706.03762  [cs.CL]. 
6. ↑ Ramachandran; Vaswani; Bello; Levskaya; Shlens (2019-06-13). «Stand-Alone Self-Attention in Vision Models». arXiv:1906.05909  [cs.CV]. 
7. ↑ Jaegle; Brock; Zisserman; Vinyals; Carreira (2021-06-22). «Perceiver: General Perception with Iterative Attention». arXiv:2103.03206  [cs.CV]. 
8. ↑ Ray, Tiernan. «Google's Supermodel: DeepMind Perceiver is a step on the road to an AI machine that could process anything and everything». ZDNet. Consultado el 19 de agosto de 2021. 
9. ↑ «Pytorch.org seq2seq tutorial». Consultado el 2 de diciembre de 2021. 
10. ↑ Schmidhuber, Jürgen (1993). «Reducing the ratio between learning complexity and number of time-varying variables in fully recurrent nets». ICANN 1993 (Springer): 460 - 463. 
11. ↑ Schlag, Imanol; Irie, Kazuki; Schmidhuber, Jürgen (2021). «Linear Transformers Are Secretly Fast Weight Programmers». ICML 2021 (Springer): 9355 - 9366. 
12. ↑ Choromanski, Krzysztof; Likhosherstov, Valerii; Dohan, David; Song, Xingyou; Gane, Andreea; Sarlos, Tamas; Hawkins, Peter; Davis, Jared; Mohiuddin, Afroz; Kaiser, Lukasz; Belanger, David; Colwell, Lucy; Weller, Adrian (2020). «Rethinking Attention with Performers». arXiv:2009.14794  [cs.CL]. 
13. ↑ Bahdanau (2016-05-19). «Neural Machine Translation by Jointly Learning to Align and Translate». arXiv:1409.0473  [cs.CL]. 
14. ↑ ^{a b} Luong (2015-09-20). «Effective Approaches to Attention-based Neural Machine Translation». arXiv:1508.04025v5  [cs.CL]. 
15. ↑ «Papers with Code - A Decomposable Attention Model for Natural Language Inference». paperswithcode.com. (en inglés). 
16. ↑ Zhu, Xizhou; Cheng, Dazhi; Zhang, Zheng; Lin, Stephen; Dai, Jifeng (2019). «An Empirical Study of Spatial Attention Mechanisms in Deep Networks». 2019 IEEE/CVF International Conference on Computer Vision (ICCV): 6687-6696. ISBN 978-1-7281-4803-8. doi:10.1109/ICCV.2019.00679. 
17. ↑ Hu, Jie (2018). «Squeeze-and-Excitation Networks». IEEE/CVF Conference on Computer Vision and Pattern Recognition: 7132-7141. ISBN 978-1-5386-6420-9. doi:10.1109/CVPR.2018.00745. 
18. ↑ Woo, Sanghyun; Park, Jongchan; Lee, Joon-Young; Kweon, In So (2018-07-18). «CBAM: Convolutional Block Attention Module». arXiv:1807.06521  [cs.CV]. 
19. ↑ Georgescu, Mariana-Iuliana; Ionescu, Radu Tudor; Miron, Andreea-Iuliana; Savencu, Olivian; Ristea, Nicolae-Catalin; Verga, Nicolae; Khan, Fahad Shahbaz (2022-10-12). «Multimodal Multi-Head Convolutional Attention with Various Kernel Sizes for Medical Image Super-Resolution». arXiv:2204.04218  [eess.IV]. 
20. ↑ Neil Rhodes (2021). CS 152 NN—27: Attention: Keys, Queries, & Values. Consultado el 22 de diciembre de 2021. «Los eventos ocurren en 06:30». 
21. ↑ Alfredo Canziani & Yann Lecun (2021). NYU Deep Learning course, Spring 2020. Consultado el 22 de diciembre de 2021. «Los eventos ocurren en 05:30». 
22. ↑ Alfredo Canziani & Yann Lecun (2021). NYU Deep Learning course, Spring 2020. Consultado el 22 de diciembre de 2021. «Los eventos ocurren en 20:15». 
23. ↑ Robertson, Sean. «NLP From Scratch: Translation With a Sequence To Sequence Network and Attention». pytorch.org. Consultado el 22 de diciembre de 2021. 

• Jurafsky, Dan; Martin, James H. (2022). «Speech and Language Processing». ch. 10.4 Attention and ch. 9.7 Self-Attention Networks: Transformers (3rd ed. draft, January 2022 edición). 
• Alex Graves (4 de mayo de 2020). «Attention and Memory in Deep Learning (videoconferencia)». DeepMind / UCL, via YouTube. 
• «Rasa Algorithm Whiteboard - Attention». YouTube.