En geometría, el hexacosicoron o 600-cell es uno de los politopos regulares convexos de 4 dimensiones, con símbolo de Schläfli {3, 3, 5}. Se lo considera a veces el análogo en cuatro dimensiones del icosaedro, razón por la cual se lo llama también hipericosaedro, porque es la figura 4D del icosaedro.
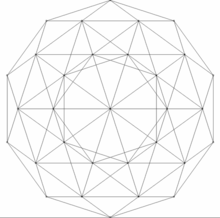

La envoltura del hexacosicoron se componen de 600 celdas en forma de tetraedro, 20 de las cuales se encuentran en cada vértice. En conjunto forman 1200 caras triangulares, 720 aristas y 120 vértices. La figura de vértice es un icosaedro. El politopo dual del hexacosicoron es el hecatonicosacoron (120-cell).
Los vértices de un hexacosicoron centrados en el origen del espacio tetradimensional, con aristas de longitud 1/φ (donde φ = (1+√5)/2 es la proporción áurea), pueden describirse como sigue:
16 vértices de la forma
- (±½, ±½, ±½, ±½),
y 8 vértices obtenidos de
- (0, 0, 0, ±1)
permutando coordenadas. Los 96 vértices finales se obtienen tomando permutaciones pares de
- ½(±1, ±φ, ±1/φ, 0).
Nótese que los primeros 16 vértices son los vértices de un teseracto, los segundos 16 son los de un hexadecacoron, y los 24 juntos forman los vértices de un icositetracoron.
Interpretados como cuaterniones, los 120 vértices forman un grupo bajo la multiplicación cuaterniónica. A este grupo se le suele llamar el grupo icosaédrico binario pues es la doble cobertura del grupo icosaédrico ordinario I. El grupo icosaédrico binario es isomorfo del grupo lineal especial SL (2,5).
El grupo de simetría del 600-cell es el grupo de Weyl de H4. Este es un grupo de orden 14400.
Véase también
La versión original de este artículo es una traducción del artículo 600-cell en Wikipedia en inglés








