El horizonte (del francés antiguo orizon, y este, vía latín, del griego ὁρίζων (horízōn) y ὅρος (hóros, “límite”)) es la línea que aparentemente separa el cielo y la tierra. Esta línea es en realidad una circunferencia en la superficie de la Tierra centrada en el observador.

En otros dominios, el horizonte se define como un plano que pasa por el centro de la Tierra y es perpendicular a la línea cenit-nadir (un radio desde el centro de la tierra hacia la superficie) o la vertical. Tal es el horizonte astronómico u horizonte racional. Los términos de su definición consideran que la esfera celeste no está centrada en el observador sino en el centro de la Tierra. Como el radio de la tierra es despreciable frente a la magnitud de la esfera celeste, este plano coincide con el plano perpendicular al radio de la Tierra que pasa por los ojos del observador.

Se definen otros tipos de horizontes atendiendo al punto de vista del observador:

• Horizonte aparente: plano ideal tangente a la superficie de la Tierra en el punto de observación.
• Horizonte sensible u horizonte real: depende del paisaje local (montañas, edificios, etc.)
• Horizonte geométrico: superficie cónica con vértice en el observador y tangente a la superficie terrestre.
• Horizonte físico u horizonte óptico: determinado por la refracción atmosférica, que permite ver por debajo del horizonte real.
• Línea del horizonte es la línea que es la proyección del final del plano del suelo o Geometral en el Plano del Cuadro, en la perspectiva cónica. En la representación coincide aproximadamente con el horizonte aparente cuando estamos al nivel del mar. Es importante al dibujar porque es el lugar donde fugan todas las rectas y los planos horizontales.

Salvo el horizonte astronómico y el horizonte aparente, todos los demás son horizontes ópticos pues están afectados por el fenómeno de la refracción.

El horizonte es un plano fundamental para algunas coordenadas celestes, por lo que de su correcto establecimiento depende la precisión de las medidas logradas. Tal es el caso de las coordenadas horizontales geocéntricas, en las que hay que tomar alturas sobre el horizonte de una estrella o de un planeta. Las medidas obtenidas in situ serán en principio referidas al horizonte aparente, y habrá que corregirlas por la refracción atmósférica y por la paralaje geocéntrica para obtener la altura referida al horizonte astronómico.

La paralaje geocéntrica —o de altura— disminuye con la altura sobre el horizonte, hasta hacerse nula en el cenit. Su corrección, para medidas de precisión, exige considerar a la Tierra como un elipsoide y no como una esfera (realmente es un geoide), tomándose el valor del radio terrestre en el punto de observación —no el radio medio—, amén de la altura sobre el suelo. Para estrellas muy lejanas la paralaje de altura puede no ser significativa.

En cuanto a la refracción, a 0º sobre el horizonte vale unos 34'. Puesto que el diámetro angular del Sol es de unos 32', cuando el disco del Sol toca el mar lo que vemos es su imagen refractada, pues el Sol está sobre nuestro horizonte óptico pero ya por debajo de nuestro horizonte geométrico. La refracción disminuye con la altura sobre el horizonte, al igual que sucedía con la paralaje de altura, anulándose en el cenit.

La palabra horizonte deriva del griego ὁρίζων κύκλος (horízōn kýklos; "límite de la rueda"^[1]​ o "círculo separador"), donde ὁρίζων es del verbo ὁρίζω (horízō) "dividir, separar", que a su vez deriva de ὅρος (hóros) "límite".^[2]​

Históricamente, la distancia al horizonte visible ha sido durante mucho tiempo vital para la supervivencia y la navegación exitosa, especialmente en el mar, porque determinaba el rango máximo de visión de un observador y, por lo tanto, de comunicación, con todas las consecuencias obvias para la seguridad y la transmisión de información que este rango implícito. Esta importancia disminuyó con el desarrollo de la radio y el telégrafo, pero aún hoy, cuando se vuela una aeronave bajo las reglas de vuelo visual, se utiliza una técnica llamada altitud de vuelo para controlar la aeronave, en la que el piloto utiliza la relación visual entre el morro de la aeronave y el horizonte para controlar la aeronave. Los pilotos también pueden conservar su orientación espacial con referencia al horizonte.

En muchos contextos, especialmente en el dibujo de perspectiva, la curvatura de la Tierra no se tiene en cuenta y el horizonte se considera la línea teórica a la que convergen los puntos de cualquier plano horizontal (cuando se proyecta sobre el plano de la imagen) a medida que aumenta su distancia del observador. Para los observadores cerca del nivel del mar, la diferencia entre este horizonte geométrico (que asume un plano de tierra infinito perfectamente plano) y el horizonte verdadero (que asume una superficie esférica de la Tierra) es imperceptible a simple vista. Sin embargo, para alguien en una colina de 1.000 m (3.300 pies) mirando al mar, el horizonte verdadero estará aproximadamente un grado por debajo de una línea horizontal.

En astronomía, el horizonte es el plano horizontal a través de los ojos del observador. Es el plano fundamental del sistema de coordenadas horizontales, el lugar geométrico de los puntos que tienen una altitud de cero grados. Si bien es similar en formas al horizonte geométrico, en este contexto un horizonte puede considerarse como un plano en el espacio, en lugar de una línea en un plano de imagen.

Suponiendo a la Tierra como una esfera perfecta (en vez de un esferoide oblato), y sin contar la refracción atmosférica, entonces la distancia al horizonte se puede calcular fácilmente.^[3]​

El teorema de la tangente-secante establece que :^[4]​

${\displaystyle \mathrm {OC} ^{2}=\mathrm {OA} \times \mathrm {OB} \,.}$

Haz las siguientes sustituciones:

• ${\displaystyle d}$ = ${\displaystyle \mathrm {OC} }$ = distancia al horizonte;
• ${\displaystyle D}$ = ${\displaystyle \mathrm {AB} }$ = diámetro de la Tierra;
• ${\displaystyle h}$ = ${\displaystyle \mathrm {OB} }$ = altura del observador sobre el nivel del mar;
• ${\displaystyle D}$ + ${\displaystyle h}$ = ${\displaystyle \mathrm {OA} }$ = diámetro de la Tierra más la altura del observador sobre el nivel del mar;

con ${\displaystyle d}$, ${\displaystyle R}$ y ${\displaystyle h}$ todos medidos en las mismas unidades. La fórmula ahora se convierte en

${\displaystyle d^{2}=h(D+h)\,\!}$

o

${\displaystyle d={\sqrt {h(D+h)}}={\sqrt {h(2R+h)}}\ ={\sqrt {2Rh+h^{2}}},}$

donde ${\displaystyle R}$ es el radio de la Tierra (6378,1 km o 3963 millas).

La misma ecuación también se puede derivar usando el teorema de Pitágoras. En el horizonte, la línea de visión ${\displaystyle {\overline {HO}}}$ es tangente a la Tierra y también es perpendicular al radio de la Tierra ${\displaystyle R}$. Esto establece un triángulo rectángulo, con la suma del radio y la altura del observador ${\displaystyle h}$ como la hipotenusa ${\displaystyle (R+h)}$. Entonces:^[3]​^[5]​^[6]​^[7]​

${\displaystyle d^{2}+R^{2}=(R+h)^{2},}$

despejando ${\displaystyle d}$:

${\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}$,

si expandimos el término ${\displaystyle (R+h)^{2}}$, los términos ${\displaystyle R^{2}}$ se cancelan y encontramos:

${\displaystyle d={\sqrt {2Rh+h^{2}}}}$

Por ejemplo, si un satélite está a una altitud de 2000 km, la distancia al horizonte es de 5430 kilómetros (3370 mi).

Si el observador está cerca de la superficie de la tierra, entonces es válido descartar ${\displaystyle h^{2}}$ en el término (${\displaystyle 2Rh+h^{2}\,}$),^[5]​^[6]​ y la fórmula se convierte en:

${\displaystyle d\approx {\sqrt {2Rh}}\,}$

Usando kilómetros para ${\displaystyle d}$ y ${\displaystyle R}$, y metros para ${\displaystyle h}$, y tomando el radio medio de la Tierra como 6371 km, la distancia al horizonte es:^[7]​

${\displaystyle d\approx {\sqrt {2\cdot 6371\cdot {h/1000}}}\approx 3.570{\sqrt {h}}\,.}$

A 1,5 metros del suelo, entonces el horizonte está a unos 4,4 km de distancia; a 10.000 m de altitud desde un avión el horizonte está a casi 360 km de distancia; y desde la Estación Espacial Internacional en órbita, a una altura de 420 km, el horizonte está a más de 2.300 km de distancia.^[7]​

Usando unidades imperiales, con ${\displaystyle d}$ y ${\displaystyle R}$ en millas (como se usa comúnmente en tierra) y ${\displaystyle h}$ en pies, la distancia al horizonte es:

${\displaystyle d\approx {\sqrt {2\cdot 3963\cdot {h/5280}}}\approx {\sqrt {1.5h}}\approx 1.22{\sqrt {h}}}$

Si d está en millas náuticas y ${\displaystyle h}$ en pies, el factor constante es aproximadamente 1,06, que está lo suficientemente cerca de 1 como para que a menudo se ignore, lo que da:

${\displaystyle d\approx {\sqrt {h}}}$

Estas fórmulas se pueden usar cuando ${\displaystyle h}$ es mucho más pequeño que el radio de la Tierra (6371 km o 3959 mi), incluidas todas las vistas desde la cima de cualquier montaña, aviones o globos de gran altitud. Con las constantes dadas, tanto las fórmulas métricas como las imperiales tienen una precisión del 1% (consulte la siguiente sección para saber cómo obtener una mayor precisión). Si ${\displaystyle h}$ es significativa con respecto a ${\displaystyle R}$, como sucede con la mayoría de los satélites, la aproximación ya no es válida y se requiere la fórmula exacta.

Si por ejemplo tomásemos una recta tangente desde el punto ${\displaystyle H}$ con 1 milla de distancia ${\displaystyle d}$ entonces mediante la anterior ecuación obtenemos que la caída de la curvatura de la Tierra ${\displaystyle h}$ sería de 0,000126 millas o 7,98 pulgadas.^[8]​ Por esta razón a veces se usa la aproximación:^[8]​^[9]​

${\displaystyle h=8{\text{ pulgadas}}\times {\text{ millas}}^{2}}$

La parábola expresada en la ecuación anterior es precisa a niveles prácticos para distancias inferiores a 400 km sin considerar la altura del observador.^[10]​ La parábola muestra un error del 21% de frente al cálculo pitagórico a esta distancia 3,960 millas.^[11]​

Dos elevaciones separadas por el horizonte pueden unirse por una línea recta que pase por encima de la curvatura de la Tierra, por lo que puede verse la parte superior de un objeto por encima del horizonte. Esta distancia no es otra que la suma de sus distancias de ambos horizonte.

Por ejemplo, si un vigía de un barco ${\displaystyle B}$ está a una altura ${\displaystyle h_{B}}$ sobre el nivel del mar, y otra persona está en un faro ${\displaystyle L}$ de una altura ${\displaystyle h_{L}}$ sobre el nivel del mar, entonces la distancia visible entre ellas ${\displaystyle D_{BL}}$ es igual a ${\displaystyle D_{B}+D_{L}}$. En consecuencia, el vigía podrá ver el faro siempre que la distancia entre ellas sea menor que:

${\displaystyle D_{B}+D_{L}<3,57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})}$

donde ${\displaystyle D_{B}+D_{L}}$ es en kilómetros y ${\displaystyle h_{B}}$ y ${\displaystyle h_{L}}$ en metros.

Si el vigía desea verificar su posición y, como único punto de referencia en su zona de navegación, ve desde el puente de mando del barco la parte superior de un faro. En la carta náutica se podrá ver tanto sea la posición geográfica así como la altura sobre el nivel del mar del faro ${\displaystyle h_{L}}$, en este ejemplo de 20 metros. Para calcular la distancia desde el barco al faro, el navegante conoce que la altura desde el nivel del mar al puente de mando donde el se encuentra, ${\displaystyle h_{B}}$ es de 6 metros, de allí, y dado que solo ve la parte superior del faro puede concluir que la parte inferior del mismo no la puede ver debido a la curvatura de la Tierra, y puede entonces calcular la distancia al faro ${\displaystyle D_{BL}}$ de la siguiente manera:

${\displaystyle D_{BL}=3,572\,({\sqrt {6}}+{\sqrt {20}})}$ o sea aproximadamente 25 km.

Como otro ejemplo, supongamos que un observador, cuya altura de sus ojos está a 2 metros del nivel del suelo usa prismáticos para mirar un edificio distante que sabe que consta de treinta pisos, cada uno de 3,5 metros de altura. Cuenta los pisos que puede ver y descubre que solo hay diez. Entonces, veinte pisos o 70 metros del edificio están ocultos para él por la curvatura de la Tierra. A partir de esto, puede calcular su distancia desde el edificio:

${\displaystyle D\approx 3.57({\sqrt {2}}+{\sqrt {70}})}$

que llega a unos 35 kilómetros.

Barco ocultándose debajo del horizonte debido a la curvatura de la Tierra. El cálculo de la distancia del horizonte permite a marineros estimar sin radar el alcance de un contacto distante entre otras naves.^[12]​

De manera similar, es posible calcular cuánto de un objeto distante es visible sobre el horizonte. Supongamos que un observador está a 10 metros sobre el nivel del mar y está observando un barco que está a 20 km de distancia. Su horizonte es:

${\displaystyle 3.57{\sqrt {10}}}$

kilómetros de él, lo que viene a unos 11,3 kilómetros de distancia. El barco está a 8,7 km más de distancia. La altura de un punto en el barco que es apenas visible para el observador está dada por:

${\displaystyle h\approx \left({\frac {8.7}{3.57}}\right)^{2}}$

que llega a casi exactamente seis metros. Por lo tanto, el observador puede ver esa parte del barco que está a más de seis metros sobre el nivel del agua. La parte de la nave que está por debajo de esta altura está oculta para él por la curvatura de la Tierra. En esta situación, se dice que el barco está hundido "casco abajo" (hull down en inglés).^[12]​

Otra relación implica la distancia ortodrómica de círculo máximo ${\displaystyle s}$ a lo largo del arco sobre la superficie curva de la Tierra hasta el horizonte; esto es más directamente comparable a la distancia geográfica en un mapa.

Se puede formular en términos de ${\displaystyle \gamma \,}$ en radianes,

${\displaystyle s=R\gamma \,;}$

entonces

${\displaystyle \cos \gamma =\cos {\frac {s}{R}}={\frac {R}{R+h}}\,}$

Resolviendo para ${\displaystyle s}$ da

${\displaystyle s=R\cos ^{-1}{\frac {R}{R+h}}\,}$

La distancia ${\displaystyle s}$ también se puede expresar en términos de la distancia de línea de visión ${\displaystyle d}$; de la segunda figura a la derecha,

${\displaystyle \tan \gamma ={\frac {d}{R}}\,;}$

sustituyendo ${\displaystyle \gamma \,}$ y reordenando da

${\displaystyle s=R\tan ^{-1}{\frac {d}{R}}\,.}$

Las distancias ${\displaystyle d}$ y ${\displaystyle s}$ son casi iguales cuando la altura del objeto es insignificante en comparación con el radio (es decir, ${\displaystyle h\ll R}$).

Cuando el observador está elevado, el ángulo cenital del horizonte puede ser superior a 90°. El ángulo cenital máximo visible se produce cuando el rayo es tangente a la superficie de la Tierra; del triángulo OCG en la figura de la derecha,

${\displaystyle \cos \gamma ={\frac {R}{R+h}}}$

dónde ${\displaystyle h}$ es la altura del observador sobre la superficie y ${\displaystyle \gamma }$ es el buzamiento angular del horizonte. Está relacionado con el ángulo cenital del horizonte ${\displaystyle z}$ por:

${\displaystyle z=\gamma +90{}^{\circ }}$

Para una altura no negativa ${\displaystyle h}$, el ángulo ${\displaystyle z}$ es siempre ≥ 90°.

Si la Tierra fuera un mundo sin aire como la Luna, la luz viajaría horizontalmente y los cálculos anteriores serían precisos. Sin embargo, la Tierra tiene una atmósfera de aire, cuya densidad e índice de refracción varían considerablemente según la temperatura y la presión. Esto hace que el aire refracte la luz en diferentes grados, afectando la apariencia del horizonte. Por lo general, la densidad del aire justo por encima de la superficie de la Tierra es mayor que su densidad a mayores altitudes. Esto hace que su índice de refracción sea mayor cerca de la superficie que más arriba, lo que hace que la luz que viaja aproximadamente horizontalmente sea refractada hacia abajo.^[13]​ Esto hace que la distancia real al horizonte sea mayor que la distancia calculada con fórmulas geométricas. Con condiciones atmosféricas estándares o normalizadas, la diferencia es de aproximadamente el 8%. Esto cambia el factor de 3,57, en las fórmulas métricas usadas arriba, a aproximadamente 3,86.^[5]​^[7]​ Esta corrección puede ser una aproximación bastante buena en condiciones atmosféricas normalizadas.

Cuando las condiciones son inusuales, esta aproximación falla. La refracción es fuertemente afectada por los gradientes de temperatura, que pueden variar considerablemente de un día a otro, especialmente sobre el agua. En casos extremos, por lo general en primavera, cuando el aire caliente supera el agua fría, la refracción puede permitir que la luz siga la superficie de la Tierra durante cientos de kilómetros. Las condiciones opuestas ocurren, por ejemplo, en desiertos, donde la superficie es muy caliente, tan caliente, el aire de baja densidad está por debajo del aire más fresco. Esto hace que la luz sea refractada hacia arriba, causando efectos de espejismo que hacen que el concepto del horizonte no tenga ningún sentido. Los valores calculados para los efectos de la refracción en condiciones inusuales son por lo tanto aproximados.^[5]​ Sin embargo, se han hecho intentos para calcularlas con mayor precisión que la aproximación simple descrita anteriormente.

Fuera del rango de longitud de onda visual, la refracción será diferente. Para el radar (por ejemplo, para longitudes de onda de 300 a 3 mm, es decir, frecuencias entre 1 y 100 GHz), el radio de la Tierra puede multiplicarse por 4/3 para obtener un radio efectivo que dé un factor de 4.12 en la fórmula métrica, es decir, 15% más allá del horizonte geométrico o 7% más allá de lo visual. El factor 4/3 no es exacto, ya que en el caso visual la refracción depende de las condiciones atmosféricas.

Por lo general el aire es más denso en la superficie, por lo que desde la altura de un observador ${\displaystyle AM}$ la línea de visión tangente a la Tierra del horizonte verdadero ${\displaystyle AT}$ se curva formando un arco la ${\displaystyle AB}$ debido a la refracción de la atmósfera, que dobla los rayos de luz hacia abajo en un arco con un radio mayor que el de la Tierra.^[10]​ En consecuancia el horizonte aparente (refractado) ${\displaystyle B}$ es más alejado que el horizonte verdadero ${\displaystyle T}$, lo que permite ver objetos que estarían ocultos por la curvatura de la Tierra.^[5]​

Es común en topografía y geodesia que si la altura del observador ${\displaystyle AM}$ es menor de 8 km, inferior a la troposfera, se supone una atmósfera homogénea en la que el rayo curvo es el arco de un círculo para facilitar los cálculos.^[5]​

Para saber el radio del arco de la luz refractada ${\displaystyle R'}$ se obtiene mediante la fracción del radio de la Tierra ${\displaystyle R}$ entre uno menos el "índice de refracción" atmosférico ${\displaystyle k}$:^[10]​^[14]​

${\displaystyle R'={R \over 1-k}}$

En una refracción estándar a nivel del mar donde ${\displaystyle k=}$ 0,17 el radio ${\displaystyle R'}$ es 7681 km. Se denomina como "constante de refracción" la relación del radio terrestre ${\displaystyle R}$ con el radio de la luz refractada ${\displaystyle R'}$.^[5]​^[15]​^[16]​ En navegación se denomina "depresión del horizonte" la diferencia del ángulo entre el horizonte verdadero ${\displaystyle D_{V}}$ y el horizonte verdadero ${\displaystyle D_{A}}$.^[17]​^[18]​^[19]​ Aproximadamente ${\displaystyle R'}$ es 7 veces el radio de la Tierra, por lo que se asume generalmente una constante de refracción de 1/7 donde ${\displaystyle R'=R\times 7/6}$, que es 7433 km.^[5]​^[10]​ Entonces mediante la ecuación anterior de la distancia exacta del horizonte se obtiene que:^[10]​^[14]​

${\displaystyle D_{\mathrm {H} }={\sqrt {(R+H_{O})^{2}-R^{2}}}}$

donde:

${\displaystyle D_{\mathrm {H} }=}$ distancia de la línea de visión al horizonte

${\displaystyle H_{O}=}$ altura del ojo del observador medida desde la superficie del globo

${\displaystyle R=}$ radio de la tierra (6371 km sin refracción; 7681 km o 7433 km para refracción estándar).

John Sweer (1938) calculó que si la densidad del perfil de las atmósferas es conocida, la distancia d del horizonte está dada por^[20]​

${\displaystyle d={{R}_{\text{E}}}\left(\psi +\delta \right)\,,}$

donde ${\displaystyle R_{E}}$ es el radio de la Tierra, ${\displaystyle \psi }$ es la inmersión del horizonte y ${\displaystyle \delta }$ es la refracción del horizonte. La inmersión es determinada de forma simple mediante a partir de

${\displaystyle \cos \psi ={\frac {{R}_{\text{E}}{\mu }_{0}}{\left({{R}_{\text{E}}}+h\right)\mu }}\,,}$

donde h es la altura sobre la Tierra del observador, ${\displaystyle \mu }$ es el índice de refracción del aire a la altura del observador, y ${\displaystyle \mu _{0}}$ es el índice de refracción de a la altura de la superficie de la Tierra.

La refracción debe ser encontrada mediante la integración de

${\displaystyle \delta =-\int _{0}^{h}{\tan \phi {\frac {{\text{d}}\mu }{\mu }}}\,,}$

donde ${\displaystyle \phi \,\!}$ es el ángulo entre el rayo y una línea a través del centro de la Tierra. Los ángulos ${\displaystyle \psi }$ y ${\displaystyle \phi \,\!}$ están relacionados mediante ${\displaystyle \phi =90{}^{\circ }-\psi \,.}$

Un enfoque mucho más simple por Andrew T. Young (2013),^[5]​ que provee esencialmente los mismos resultados que la aproximación de primero orden presentada arriba, utiliza el modelo geométrico pero utiliza un radio de ${\displaystyle R'=R\times 7/6}$. La distancia al horizonte es entonces

${\displaystyle d={\sqrt {2R^{\prime }h}}\,.}$

Tomando el radio de la Tierra como 6371 km, con d en kilómetros y h en metros,

${\displaystyle d\approx 3.86{\sqrt {h}}\,;}$

con d en millas y h en pies,

${\displaystyle d\approx 1.32{\sqrt {h}}\,.}$

Los resultados del método de Young son bastante cercanos a los del método de Sweer, y son suficientemente exactos para la mayoría de los propósitos.

Para unidades inglesas existe una vieja regla data por R. Langton Cole (1913), donde:^[5]​^[21]​

${\displaystyle distancia\ al\ horizonte\ (millas)={\sqrt {7\times h\ (pies)/4}}}$

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Horizonte» – noticias · libros · académico · imágenes Este aviso fue puesto el 7 de mayo de 2023.

Desde un punto por encima de la superficie de la Tierra, el horizonte parece ligeramente convexo; es un arco circular. La siguiente fórmula expresa la relación geométrica básica entre esta curvatura visual, la altitud, y el radio de la Tierra:

${\displaystyle \kappa ={\sqrt {\left(1+{\frac {h}{R}}\right)^{2}-1}}\ }$

La curvatura es el recíproco del radio angular de la curvatura en radianes. Una curvatura de 1,0 aparece como un círculo de un radio angular de 57,3° correspondiente a una altitud de aproximadamente 2640 km (1640 millas) sobre la superficie de la Tierra. A una altitud de 10 km (6,2 millas; 33 000 pies), la altitud de crucero de un avión típico, la curvatura matemática del horizonte es de aproximadamente 0,056, la misma curvatura del borde del círculo con un radio de 10 m que se ve desde 56 cm directamente sobre el centro del círculo. Sin embargo, la curvatura aparente es menor que la debida a la refracción de la luz por la atmósfera y el oscurecimiento del horizonte por las altas capas de nubes que reducen la altitud sobre la superficie visual.

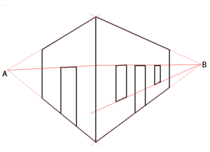
El horizonte es una característica clave del plano pictórico en la ciencia de la perspectiva gráfica. Suponiendo que el plano de la imagen está vertical al suelo y que P es la proyección perpendicular del punto del ojo O en el plano de la imagen, el horizonte se define como la línea horizontal que pasa por P. El punto P es el punto de fuga de las líneas perpendiculares a la imagen. Si S es otro punto en el horizonte, entonces es el punto de fuga de todas las líneas paralelas a OS. Pero Brook Taylor (1719) indicó que el plano del horizonte determinado por O y el horizonte era como cualquier otro plano:

El término de Línea Horizontal, por ejemplo, es apto para confinar las Nociones de un Aprendiz al Plano del Horizonte, y hacerle imaginar que ese Plano disfruta de algunos Privilegios particulares, que hacen que las Figuras en él sean más fáciles y más convenientes. ser descrito, por medio de esa Línea Horizontal, que las Figuras en cualquier otro plano;... Pero en este Libro no hago diferencia entre el Plano del Horizonte, y cualquier otro Plano cualquiera...^[22]​^[23]​

La peculiar geometría de la perspectiva donde las líneas paralelas convergen en la distancia, estimuló el desarrollo de la geometría proyectiva que postula un punto en el infinito donde las líneas paralelas se encuentran. En su libro Geometry of an Art (2007), Kirsti Andersen describió la evolución del dibujo en perspectiva y la ciencia hasta 1800, señalando que los puntos de fuga no tienen por qué estar en el horizonte. En un capítulo titulado "Horizonte", John Stillwell contó cómo la geometría proyectiva ha llevado a la geometría de incidencia, el estudio abstracto moderno de la intersección de líneas. Stillwell también se aventuró en los fundamentos de las matemáticas en una sección titulada "¿Cuáles son las leyes del álgebra?" El "álgebra de puntos", propuesta originalmente por Karl von Staudt que derivaba los axiomas de un campo, fue deconstruida en el siglo XX, dando lugar a una amplia variedad de posibilidades matemáticas. Stillwell afirma

Este descubrimiento de hace 100 años parece capaz de dar la vuelta a las matemáticas, aunque aún no ha sido absorbido por completo por la comunidad matemática. No solo desafía la tendencia de convertir la geometría en álgebra, sino que sugiere que tanto la geometría como el álgebra tienen una base más simple de lo que se pensaba anteriormente.^[24]​

• Cenit
• Nadir
• Acimut
• Tierra esférica

• Young, Andrew T. «Dip of the Horizon». Green Flash website (Sections: Astronomical Refraction, Horizon Grouping) (San Diego State University Department of Astronomy). Consultado el 16 de abril de 2011. 
• Esta obra contiene una traducción derivada de «Horizon» de Wikipedia en inglés, concretamente de esta versión del 25 de abril de 2023, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

• Distance of the Horizon/ Geographic Range Home Page
• «Earth Curvature Calculator - Calculate the curve you should see». earthcurvature.com. 
• «Earth Curvature Calculator». www.omnicalculator.com. 
• «Earth Curve Calculator». dizzib.github.io. 
• «Earth Curvature Calculator - Calculate the curve you should see». earthcurvature.com. 
• u/darkstarq. «Horizon Calculator». GeoGebra. 
• «Metabunk: Earth's Curve Horizon, Bulge, Drop, and Hidden Calculator». Metabunk. 
• «Finding the Curvature of the Earth: Stand-Alone App». walter.bislins.ch. 

A partir de la tercera se toma en cuenta la altura del observador. Las dos últimas también toman la refracción atmosférica como factor.