En matemáticas, en particular en álgebra homológica y otras aplicaciones de la teoría de categorías abelianas, el lema de los cinco es un lema importante y ampliamente usado dentro de la teoría de diagramas conmutativos. Es válido no solamente para categorías abelianas sino que también funciona en la categoría de grupos, por ejemplo.

El lema de los cinco puede pensarse como una combinación de otros dos lemas, los llamados lemas de los cuatro, que son duales uno del otro.

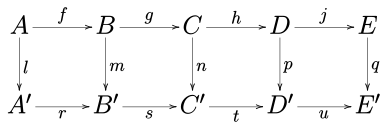
Considérese el siguiente diagrama conmutativo dentro de una categoría abeliana (como por ejemplo la de los grupos abelianos o la de los espacios vectoriales sobre un cuerpo dado) o en la categoría de grupos.

El lema de los cinco afirma que, si las filas son secuencias exactas, m y p son isomorfismos, l es un epimorfismo y q es un monomorfismo, entonces n es también un isomorfismo.

Los dos lemas de los cuatro afirman:
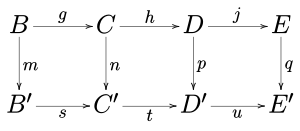
(1) Si las filas del diagrama conmutativo

son secuencias exactas y m y p son epimorfismos y además q es un monomorfismo, entonces n es un epimorfismo.

(2) Si las filas del diagrama conmutativo

son exactas y m y p son monomorfismos y además l es un epimorfismo, entonces n es un monomorfismo.

El método usado en la demostración se denomina comúnmente persecución de diagramas.^[1]​ Se demostrará el lema de los cinco probando separadamente cada uno de los dos lemas de los cuatro.

Para la persecución de diagramas, se asumirá que existe una categoría de módulos sobre un cierto anillo, de tal manera que puede hablarse de elementos de los objetos en el diagrama y considerar que los morfismos del diagrama son funciones (de hecho, homomorfismos) que actúan sobre esos elementos.

En general, se define monomorfismo como un homomorfismo inyectivo; y se define epimorfismo como un homomorfismo suprayectivo. De manera similar, para tratar con la condición de exactitud, puede pensarse en el núcleo y la imagen en el sentido de la teoría de funciones. La demostración se aplicaría a cualquier categoría abeliana debido al teorema del encaje de Mitchell, que afirma que cualquier categoría abeliana pequeña puede representarse como una categoría de módulos sobre cierto anillo. Para la categoría de grupos, conviértase toda la notación aditiva en una notación que involucre el producto del grupo, y nótese que la conmutatividad del grupo abeliano no se usa explícitamente nunca.

Así, para probar (1), asúmase que m y p son suprayectivos y q es inyectivo.

• Sea c′ un elemento de C′.
• Puesto que p es suprayectivo, entonces existe un elemento d en D que cumple que p(d) = t(c′).
• Por la conmutatividad del diagrama, u(p(d)) = q(j(d)).
• Puesto que im t = ker u por la exactitud, 0 = u(t(c′)) = u(p(d)) = q(j(d)).
• Puesto que q es inyectivo, j(d) = 0, de tal manera que d está en ker j = im h.
• Por tanto, existe un c en C que cumple h(c) = d.
• Entonces t(n(c)) = p(h(c)) = t(c′). Puesto que t es un homomorfismo, se sigue que t(c′ - n(c)) = 0.
• Por la exactitud, c′ - n(c) pertenece a la imagen de s, por lo que existe un b′ en B′ tal que s(b′) = c′ - n(c).
• Puesto que m es suprayectivo, podemos encontrar un b de B tal que b′ = m(b).
• Por la conmutatividad, n(g(b)) = s(m(b)) = c' - n(c).
• Puesto que n es un homomorfismo, n(g(b) + c) = n(g(b)) + n(c) = c′ - n(c) + n(c) = c′.
• Por tanto, n es suprayectivo.

Entonces, para demostrar (2), asúmase que m y p son inyectivos y que l es suprayectivo.

• Sea un c de C tal que n(c) = 0.
• t(n(c)) es entonces 0.
• Por la conmutatividad, p(h(c)) = 0.
• Puesto que p es inyectivo, h(c) = 0.
• Por la exactitud, existe un elemento b de B tal que g(b) = c.
• Por la conmutatividad, s(m(b)) = n(g(b)) = n(c) = 0.
• Por la exactitud, existe entonces un elemento a′ de A′ tal que r(a′) = m(b).
• Puesto que l es supryectivo, existe un a de A tal que l(a) = a′.
• Por la conmutatividad, m(f(a)) = r(l(a)) = m(b).
• Puesto que m es inyectivo, f(a) = b.
• Así c = g(f(a)).
• Puesto que la composición de g y f es trivial, c = 0.
• Por tanto, n es inyectivo.

Combinando los dos lemas de los cuatro se tiene que el homomorfismo n es tanto epimorfismo como monomorfismo y, por tanto, es un isomorfismo.

El lema de los cinco se usa aplica frecuentemente a secuencias exactas largas, cuando se calcula la homología o la cohomología de un cierto objeto. Así se uno emplea un subojeto más simple cuya homología o cohomología sea conocida y llega a una secuencia exacta que involucre los grupos de homología desconocidos, pero si uno puede comparar el objeto original y el sub-objeto con algunos bien conocidos mediante morfismos, entonces se induce un morfismo entre las respectivas secuencias largas y el lema de los cinco puede usarse para determinar los grupos de homología desconocidos.

• Lema de los cinco abreviado, un caso especial del lema de los cinco para secuencias exactas breves.
• Lema de la serpiente, otro lema demostrado mediante "persecución de diagramas".
• Lema de los nueve

• W. R. Scott: Group Theory, Prentice Hall, 1964.
• Massey, William S. (1991). A basic course in algebraic topology. Graduate texts in mathematics 127 (3rd edición). Springer. ISBN 978-0-387-97430-9.