
En física, la masa crítica es la cantidad mínima de material necesaria para que se mantenga una reacción nuclear en cadena. La masa crítica de una sustancia fisible depende de sus propiedades físicas (en particular su densidad) y nucleares (su enriquecimiento y sección eficaz de fisión), su geometría (su forma) y su pureza, además de si está rodeada o no por un reflector de neutrones. Al rodear a un material fisible por un reflector de neutrones la masa crítica resulta menor. En el caso de una esfera rodeada por un reflector de neutrones, la masa crítica es de unos cincuenta y dos kilogramos para el uranio 235 y de diez kilogramos para el plutonio 239.[1]
"Crítico" se refiere a un estado de equilibrio dinámico en la reacción de fisión en cadena; en él no existe aumento de la potencia, temperatura y densidad de neutrones en el tiempo. "Subcrítico" se refiere a la incapacidad de mantener o sostener en el tiempo una reacción nuclear en cadena; al introducir una cierta cantidad de neutrones en un conjunto subcrítico, la población de neutrones disminuirá a lo largo del tiempo (por fenómenos de absorción en el material o por fuga). "Supercrítico" se refiere a un sistema en el que la cantidad de procesos de fisión por unidad de tiempo aumenta hasta el punto en que algún mecanismo de realimentación intrínseco hace que el reactor alcance un punto de equilibrio dinámico (se ponga crítico) a una mayor temperatura o potencia o se destruya (en cuyo caso se desarma el conjunto crítico).
Es posible que un conjunto alcance el estado de crítico a potencias muy próximas a cero. Si fuera posible hacer un experimento en el que se agregue una cantidad exacta de material fisible a una masa levemente subcrítica, se podría crear un conjunto con una masa exactamente crítica, y en ese caso la reacción en cadena de fisión mantendría exactamente una generación de neutrones (ya que el consumo del combustible producido por el mismo proceso de fisión tornaría al conjunto nuevamente subcrítico).
Esfera desnuda de un isótopo

La esfera es la forma que posee menor masa crítica. Es posible reducir la masa crítica si se rodea la esfera con un material reflector de neutrones, o algún otro material.
En el caso de una esfera desnuda (sin reflector de neutrones) la masa crítica es de más de 50 kg para el uranio-235 y 10 kg para el plutonio-239.
La siguiente tabla presenta la masa crítica de esferas desnudas de algunos isótopos con vidas medias de más de 100 años.
| Nucleido | Vida media (y) |
Masa crítica (kg) |
Diámetro (cm) |
Ref |
|---|---|---|---|---|
| Protactinio-231 | 750±180 | |||
| Uranio-233 | 159,200 | 15 | 11 | [2] |
| Uranio-235 | 703,800,000 | 52 | 17 | [2] |
| Neptunio-236 | 154,000 | 7 | 8.7 | [3] |
| Neptunio-237 | 2,144,000 | 60 | 18 | [4][5] |
| Plutonio-238 | 87.7 | 9.04–10.07 | 9.5–9.9 | [6] |
| Plutonio-239 | 24,110 | 10 | 9.9 | [2][6] |
| Plutonio-240 | 6561 | 40 | 15 | [2] |
| Plutonio-241 | 14.3 | 12 | 10.5 | [7] |
| Plutonio-242 | 375,000 | 75–100 | 19–21 | [7] |
| Americio-241 | 432.2 | 55–77 | 20–23 | [8] |
| Americio-242m | 141 | 9–14 | 11–13 | [8] |
| Americio-243 | 7370 | 180–280 | 30–35 | [8] |
| Curio-243 | 29.1 | 7.34–10 | 10–11 | [9] |
| Curio-244 | 18.1 | 13.5–30 | 12.4–16 | [9] |
| Curio-245 | 8500 | 9.41–12.3 | 11–12 | [9] |
| Curio-246 | 4760 | 39–70.1 | 18–21 | [9] |
| Curio-247 | 15,600,000 | 6.94–7.06 | 9.9 | [9] |
| Berkelio-247 | 1380 | 75.7 | 11.8-12.2 | [10] |
| Berkelio-249 | 0.9 | 192 | 16.1-16.6 | [10] |
| Californio-249 | 351 | 6 | 9 | [3] |
| Californio-251 | 900 | 5.46 | 8.5 | [3] |
| Californio-252 | 2.6 | 2.73 | 6.9 | [11] |
| Einstenio-254 | 0.755 | 9.89 | 7.1 | [10] |
La masa crítica del uranio depende del grado en que este presente (enriquecido) en el isótopo uranio-235: para un enriquecimiento del 20 % de U-235 la masa crítica es de más de 400 kg; para el 15 % de U-235, la masa crítica excede los 600 kg.
La masa crítica es inversamente proporcional al cuadrado de la densidad: si por ejemplo la densidad se incrementa en un 1 % la masa crítica se reducirá en un 2 %, entonces el volumen será menor en un 3 % y el diámetro se reducirá en 1 %. La probabilidad de que un neutrón por cm recorrido colisione con un núcleo es proporcional a la densidad, o sea aumentaría en nuestro ejemplo en un 1 %, lo cual compensa el hecho que la distancia recorrida antes de que el neutrón salga del sistema es un 1 % menor. Esto es algo que debe tenerse en cuenta al realizar cálculos más precisos de las masas críticas de los isótopos del plutonio que los valores indicativos que se muestran en la tabla previa, porque el plutonio tiene un gran número de fases cristalinas cuyas densidades son sumamente distintas entre sí.
Es importante notar que no todos los neutrones contribuyen a la reacción en cadena. Algunos escapan al sistema, y otros pueden sufrir capturas radioactivas.
Sea q la probabilidad que un dado neutrón origine una fisión en un núcleo. Considerando en forma simplificada sólo a los neutrones prontos o instantáneos, y si se llama ν al número de neutrones prontos generados en la fisión nuclear de un átomo. Por ejemplo, en el caso del uranio-235 ν = 2.7. Por lo tanto la criticidad tendrá lugar cuando νq = 1. La dependencia con la geometría, la masa y la densidad se manifiesta a través del factor q.
Si se considera la sección eficaz total de interacción (usualmente medida en barn), entonces el camino libre medio de un neutrón pronto se expresa como donde es la densidad de número atómico. La mayoría de las interacciones son choques con cambio de dirección y energía del neutrón, de forma tal que un neutrón recorrerá una trayectoria aleatoria hasta que escape del medio en el que se encuentra o produzca una reacción de fisión. En la medida en que los otros mecanismos de desaparición de neutrones no sean significativos, entonces el radio de la esfera de masa crítica se puede calcular en forma aproximada como el producto del camino libre medio y la raíz cuadrada de uno más la cantidad de eventos de colisión por evento de fisión (lo que llamamos ), dado que la distancia neta recorrida en un recorrido aleatorio es proporcional a la raíz cuadrada de la cantidad de pasos que se dan:
Donde, es necesario recordar nuevamente, que esto es solo un estimación gruesa.
La criticidad se puede expresar en función de la masa total M, la masa nuclear m, la densidad ρ, y un factor f que incluye los efectos geométricos y de otro tipo como:
En donde queda confirmado la dependencia de la masa crítica con la inversa del cuadrado de la densidad tal como se mencionó previamente.
Alternativamente, esto se puede expresar en forma más sucinta en función de la densidad superficial de núcleos Σ:
Donde se reescribió el factor f como f' para tener en cuenta que los dos valores pueden diferir dependiendo de efectos geométricos y de como se defina Σ. Por ejemplo, para una esfera sólida desnuda de Pu-239 la criticidad se obtiene a 320 kg/m², independientemente de la densidad, y para U-235 a 550 kg/m². O sea que la criticidad depende de que un neutrón típico "vea" una cierta cantidad de núcleos alrededor de él de manera que la densidad superficial de núcleos este por encima de un cierto valor umbral.
Esto se aplica en las armas nucleares del tipo de implosión, donde una masa esférica de material físil que es significativamente menos que la masa crítica, se vuelve supercrítica mediante un rápido aumento de (y en consecuencia también de ), ver la próxima sección. En efecto, los programas de armas nucleares más sofisticados permiten fabricar dispositivos funcionales con menos material que el requerido en los dispositivos más primitivos.
Más allá de las matemáticas, este resultado puede ser explicado mediante una simple analogía física. Si se considera el humo que expele un motor diésel por el caño de escape, inicialmente el humo parece negro, pero luego gradualmente es posible ver a través de él sin inconvenientes. Esto no se debe a que se haya modificado la sección eficaz de scattering de todas las partículas de hollín, pero en cambio a que el hollín se ha dispersado en el aire. Si se considera un cubo transparente cuyo lado es , lleno con hollín, entonces la profundidad óptica de este medio es inversamente proporcional al cuadrado de , y por lo tanto proporcional a la densidad superficial de las partículas de hollín: es posible ver a través de este cubo imaginario solo con hacer mayor el cubo (sin variar la cantidad total de hollín contenido en él).
Varias incertezas contribuyen a la determinación de un valor preciso de las masas críticas, incluyendo (1) conocimiento preciso de las secciones eficaces, (2) cálculo de los efectos geométricos. Este último problema es el que dio un fuerte impulso al desarrollo del método Montecarlo en física computacional por Nicholas Metropolis y Stanislaw Ulam. En efecto, aún para una esfera homogénea sólida, el cálculo exacto no es para nada trivial. Finalmente es de notar que el cálculo podría ser realizado si se supusiera una aproximación de un medio continuo para el transporte de neutrones, de forma tal que el problema se reduce a un problema de difusión. Sin embargo, como las dimensiones típicas del problema no son significativamente más largas que el camino libre medio, dicha aproximación tiene muy poca utilidad práctica.
Finalmente, debe notarse que para ciertas geometrías ideales, la masa crítica desde un punto de vista formal podría ser infinita, y entonces se utilizan otros parámetros para describir la criticidad. Por ejemplo, si se considera el caso de una placa infinita de material fisionable. Para todo espesor finito, esto se corresponde con una masa infinita. Sin embargo, la criticidad es solo alcanzable cuando el espesor de la placa excede un valor crítico.
Diseño de explosivos
Una bomba atómica debe almacenarse en una configuración subcrítica hasta el momento en que se la desee detonar. En el caso de una bomba de uranio, basta con mantener el combustible en forma de piezas separadas, la dimensión de cada una de ellas es menor que el tamaño crítico tanto porque sean muy pequeñas o porque sus formas previenen alcanzar la criticidad. Para producir la detonación, las partes de uranio se juntan rápidamente. En Little Boy, esto se realizó disparando una pequeña parte de uranio desde un cañón tipo arma de fuego hacia un agujero correspondiente ubicado en un pedazo mayor de uranio, un diseño conocido como bomba de fisión de tipo revolver.
También sería posible construir un explosivo de Pu-239 con una pureza teórica del 100 %. Pero en la realidad esto no es práctico porque el Pu-239 "de calidad armamento" está contaminado con pequeñas cantidades de Pu-240, el cual posee una fuerte tendencia hacia la fisión espontánea. Por esta razón, en un arma del tipo revólver se produciría una reacción nuclear antes de que las masas de plutonio estuvieran en la posición adecuada para producir una explosión de magnitud. Aun teniendo en cuenta la impureza en Pu-240, se podría en principio construir un arma tipo revólver. Sin embargo no sería un arma demasiado práctica, ya que debería ser muy larga para acelerar la masa de plutonio a muy altas velocidades para compensar los efectos mencionados anteriormente.
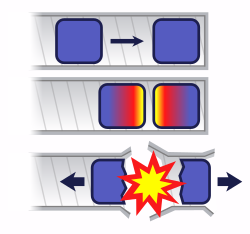
Por ello es que se recurre a otro método. El plutonio se coloca en forma de una esfera subcrítica (o con otra forma), la cual puede o no ser hueca. La detonación se produce haciendo explotar una carga de un explosivo convencional que rodea la esfera, aumentando así su densidad (y haciendo colapsar la cavidad interna si es que la hubiera) para producir una configuración que es supercrítica. A este método se lo llama arma de implosión.
Véase también
Referencias
- ↑ Serber, Robert, The Los Alamos Primer: The First Lectures on How to Build an Atomic Bomb, (University of California Press, 1992) ISBN 0-520-07576-5 Original 1943 "LA-1", declassified in 1965, plus commentary and historical introduction
- ↑ a b c d Nuclear Weapons Design & Materials, The Nuclear Threat Initiative website. Archivado el 25 de febrero de 2011 en Wayback Machine.[fuente cuestionable]
- ↑ a b c Final Report, Evaluation of nuclear criticality safety data and limits for actinides in transport, Republic of France, Institut de Radioprotection et de Sûreté Nucléaire, Département de Prévention et d'étude des Accidents.
- ↑ Chapter 5, Troubles tomorrow? Separated Neptunium 237 and Americium, Challenges of Fissile Material Control (1999), isis-online.org
- ↑ P. Weiss (26 de octubre de 2002). «Neptunium Nukes? Little-studied metal goes critical». Science News 162 (17): 259. doi:10.2307/4014034. Archivado desde el original el 15 de diciembre de 2012. Consultado el 7 de noviembre de 2013.
- ↑ a b Updated Critical Mass Estimates for Plutonium-238, U.S. Department of Energy: Office of Scientific & Technical Information
- ↑ a b Amory B. Lovins, Nuclear weapons and power-reactor plutonium, Nature, Vol. 283, No. 5750, pp. 817–823, February 28, 1980
- ↑ a b c Dias, Hemanth; Tancock, Nigel; Clayton, Angela (2003). «Critical Mass Calculations for 241Am, 242m Am and 243Am». Challenges in the Pursuit of Global Nuclear Criticality Safety. Proceedings of the Seventh International Conference on Nuclear Criticality Safety II. Tokai, Ibaraki, Japan: Japan Atomic Energy Research Institute. pp. 618-623.
- ↑ a b c d e Okuno, Hiroshi; Kawasaki, Hiromitsu (2002). «Critical and Subcritical Mass Calculations of Curium-243 to -247 Based on JENDL-3.2 for Revision of ANSI/ANS-8.15». Journal of Nuclear Science and Technology 39 (10): 1072-1085. doi:10.1080/18811248.2002.9715296.
- ↑ a b c Institut de Radioprotection et de Sûreté Nucléaire: "Evaluation of nuclear criticality safety. data and limits for actinides in transport", p. 16
- ↑ Carey Sublette, Nuclear Weapons Frequently Asked Questions: Section 6.0 Nuclear Materials February 20, 1999



















