Los números preferentes, también conocidos como valores preferentes, son una guía estándar utilizada en diseño industrial para seleccionar valores característicos de un producto.

Durante la fase de diseño, los desarrolladores de productos deben definir valores tales como largo, ancho, volumen, distancia, diámetro, y otros parámetros característicos del producto en desarrollo. Si bien estos valores están determinados por consideraciones de funcionalidad, usabilidad, compatibilidad, seguridad o costo, usualmente hay cierta libertad en el momento de seleccionar el valor exacto de un parámetro o magnitud. Los números preferentes brindan una serie de guías para seleccionar el valor final que asegure ciertas características estándar y de compatibilidad entre diseños y partes.

Los números preferentes tienen una doble finalidad:

1. Su uso incrementa la probabilidad de que otros diseñadores hagan la misma selección. Esto es particularmente útil cuando los valores seleccionados afectan la compatibilidad. Por ejemplo, si el diámetro interno de una olla, o la distancia entre tornillos de algún elemento que se fije a la pared, son seleccionados a partir de una serie de números preferentes, es muy probable que las tapas de las ollas anteriores o las perforaciones existentes en la pared se puedan reutilizar cuando se reemplace el producto original.
2. Los números preferentes son tales que cuando un producto es fabricado en diferentes tamaños los mismos se encuentran aproximadamente equidistantemente espaciados en una escala logarítmica. En consecuencia, se minimiza la cantidad de diferentes tamaños que deben ser manufacturados o almacenados.

El ingeniero de la armada francesa y coronel Charles Renard propuso en 1870 un conjunto de números preferentes a ser utilizados junto con el sistema métrico decimal. Su sistema se adoptó en 1952 como el estándar internacional ISO 3. El sistema de Renard divide el intervalo entre 1 a 10 en 5, 10, 20, o 40 pasos. El factor entre dos números consecutivos en las series de Renard es constante (antes de redondear), sea la raíz quinta, décima, vigésima o cuatrigésima de 10 (1.58, 1.26, 1.12, y 1.06 respectivamente), lo que genera una secuencia geométrica. De esta forma, el máximo error relativo es minimizado si un número arbitrario es reemplazado por el número de Renard más cercano multiplicado por la potencia de 10 apropiada.

Los números de Renard son el resultado redondeado de la fórmula:

${\displaystyle R(i,b)=10^{\frac {i}{b}}}$,

donde b es el valor de la serie seleccionada (por ejemplo b = 40 para la serie R40), e i es el i-ésimo elemento de esta serie (donde i = 0 para el inicio).

La serie básica (R5) consiste en los siguientes cinco números redondeados:

  R5: 1.00        1.60        2.50        4.00        6.30

Ejemplo: Asumamos que una restricción establece que dos tornillos deben estar separados entre 32 mm y 55 mm, seleccionaremos 40 mm, pues 4 es el siguiente número en la tabla.

Ejemplo: Se desea fabricar un conjunto de clavos con tamaños entre 15 mm y 300 mm, al utilizar la serie R5 obtendríamos los siguientes largos: 16 mm, 25 mm, 40 mm, 63 mm, 100 mm, 160 mm, y 250 mm.

Si el producto requiere mayor detalle o resolución, se pueden agregar otros cinco números a la serie, uno después de cada uno de los números de la serie original:

 R10: 1.00  1.25  1.60  2.00  2.50  3.15  4.00  5.00  6.30  8.00

el nivel de resolución de la serie puede incrementarse según sea necesario:

 R20: 1.00  1.25  1.60  2.00  2.50  3.15  4.00  5.00  6.30  8.00
        1.12  1.40  1.80  2.24  2.80  3.55  4.50  5.60  7.10  9.00

 R40: 1.00  1.25  1.60  2.00  2.50  3.15  4.00  5.00  6.30  8.00
       1.06  1.32  1.70  2.12  2.65  3.35  4.25  5.30  6.70  8.50 
        1.12  1.40  1.80  2.24  2.80  3.55  4.50  5.60  7.10  9.00
         1.18  1.50  1.90  2.36  3.00  3.75  4.75  6.00  7.50  9.50

 R80: 1.00  1.25  1.60  2.00  2.50  3.15  4.00  5.00  6.30  8.00
       1.03  1.28  1.65  2.06  2.58  3.25  4.12  5.15  6.50  8.25
        1.06  1.32  1.70  2.12  2.65  3.35  4.25  5.30  6.70  8.50
         1.09  1.36  1.75  2.18  2.72  3.45  4.37  5.45  6.90  8.75 
          1.12  1.40  1.80  2.24  2.80  3.55  4.50  5.60  7.10  9.00
           1.15  1.45  1.85  2.30  2.90  3.65  4.62  5.80  7.30  9.25
            1.18  1.50  1.90  2.36  3.00  3.75  4.75  6.00  7.50  9.50
             1.22  1.55  1.95  2.43  3.07  3.87  4.87  6.15  7.75  9.75

En algunas aplicaciones es deseable contar con valores redondeados, ya sea porque los números de la serie normal podrían entrañar niveles de precisión ficticios, o porque se necesita un valor entero (por ejemplo, la cantidad de dientes en un engranaje). Para estos casos la ISO 3 define versiones más redondeadas de la serie de Renard:

 R5": 1           1.5         2.5         4           6

R10': 1     1.25  1.6   2     2.5   3.2   4     5     6.3   8

R10": 1     1.2   1.5   2     2.5   3     4     5     6     8

R20': 1     1.25  1.6   2     2.5   3.2   4     5     6.3   8
        1.1   1.4   1.8   2.2   2.8   3.6   4.5   5.6   7.1    9 

R20": 1     1.2   1.6   2     2.5   3     4     5     6     8   
        1.1   1.4   1.8   2.2   2.8   3.5   4.5   5.5   7      9 

R40': 1     1.25  1.6   2     2.5   3.2   4     5     6.3   8
       1.05  1.3   1.7   2.1   2.6   3.4   4.2   5.3   6.7    8.5 
        1.1   1.4   1.8   2.2   2.8   3.6   4.5   5.6   7.1    9 
         1.2   1.5   1.9   2.4   3     3.8   4.8   6     7.5    9.5

Como los números de Renard se repiten después de 10 pasos o tras un cambio de escala, son idóneos para utilizarse con unidades del Sistema Internacional. No hay diferencia en utilizar las series de Renard con metros o kilómetros. Pero cuando se utiliza la serie con unidades tales como yardas o millas es muy posible que se obtengan dos conjuntos de dimensiones "bien" espaciadas pero incompatibles.

El nivel de resolución de la serie R5 puede ser demasiado elevado para algunas aplicaciones. En estos casos, algunas veces una alternativa puede ser la serie 1-2-5, aunque es algo tosca:

 ... 0.1  0.2  0.5  1  2  5  10  20  50  100  200  500  1000 ...

Esta serie cubre una década (relación de 1:10) en tres pasos. Valores adyacentes difieren por factores de 2 o 2.5.

A diferencia de las series de Renard, la serie 1-2-5 no ha sido adoptada formalmente como un estándar internacional. La serie Renard R10 puede usarse para extender la serie 1-2-5 cuando se necesita una graduación más fina.

Las denominaciones de las divisas más modernas siguen una serie 1-2-5. Una excepción son algunas monedas de valor ¼, como en los Estados Unidos y Canadá (llamada "quarter dollar" en lugar de 25 centavos). La serie ¼-½-1 (... 0.1 0.25 0.5 1 2.5 5 10 ...) es usada por las divisas derivadas del antiguo Florín neerlandés (Florín arubeño, Florín de las Antillas Neerlandesas, Dólar surinamés), algunas divisas del Medio Oriente (Dinar iraquí y el Dinar jordano, la Lira libanesa y la Lira siria), y la Rupia de los Seychellois. Sin embargo, los nuevos billetes que han introducido en el Líbano y en Siria debido a la inflación siguen la serie 1-2-5.^{[cita requerida]} El Euro, introducido en España en el año 2000, sigue la pauta 1-2-5 desde la monedita de un céntimo hasta el billete de 500 Euros.

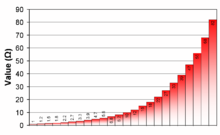
El estándar internacional IEC 60063 define otra serie de números preferentes que es comúnmente utilizado por componentes electrónicos, especialmente resistencias y condensadores. Esta serie funciona en forma similar a una serie Renard, con la excepción de que el intervalo entre 1 y 10 se subdivide en 6, 12, 24, o más pasos. Estas subdivisiones aseguran que si un número aleatorio es substituido por el número preferente más próximo, el máximo error será de 20%, 10% o 5%.

El uso de las series E está en la mayoría de los casos restringida a las resistencias y los condensadores. Para definir dimensiones para otros productos se utilizan las series de Renard (por ejemplo los fusibles), o existen estándares creados para los productos más relevantes (por ejemplo el IEC 60228 para cables).

Los números del IEC 60063 son:

E6  ( 20%): 10    15    22    33    47    68

E12 ( 10%): 10 12 15 18 22 27 33 39 47 56 68 82

E24 (  5%): 10 11 12 13 15 16 18 20 22 24 27 30
            33 36 39 43 47 51 56 62 68 75 82 91

E48 (  2%): 100 105 110 115 121 127 133 140
            147 154 162 169 178 187 196 205
            215 226 237 249 261 274 287 301
            316 332 348 365 383 402 422 442
            464 487 511 536 562 590 619 649
            681 715 750 787 825 866 909 953             

E96 (  1%): 100 102 105 107 110 113 115 118
            121 124 127 130 133 137 140 143
            147 150 154 158 162 165 169 174
            178 182 187 191 196 200 205 210
            215 221 226 232 237 243 249 255
            261 267 274 280 287 294 301 309
            316 324 332 340 348 357 365 374
            383 392 402 412 422 432 442 453
            464 475 487 499 511 523 536 549
            562 576 590 604 619 634 649 665
            681 698 715 732 750 768 787 806
            825 845 866 887 909 931 953 976

E192 (0.5%) 100 101 102 104 105 106 107 109
            110 111 113 114 115 117 118 120 
            121 123 124 126 127 129 130 132 
            133 135 137 138 140 142 143 145 
            147 149 150 152 154 156 158 160 
            162 164 165 167 169 172 174 176 
            178 180 182 184 187 189 191 193 
            196 198 200 203 205 208 210 213 
            215 218 221 223 226 229 232 234 
            237 240 243 246 249 252 255 258 
            261 264 267 271 274 277 280 284 
            287 291 294 298 301 305 309 312 
            316 320 324 328 332 336 340 344 
            348 352 357 361 365 370 374 379 
            383 388 392 397 402 407 412 417 
            422 427 432 437 442 448 453 459 
            464 470 475 481 487 493 499 505 
            511 517 523 530 536 542 549 556 
            562 569 576 583 590 597 604 612 
            619 626 634 642 649 657 665 673 
            681 690 698 706 715 723 732 741 
            750 759 768 777 787 796 806 816 
            825 835 845 856 866 876 887 898 
            909 920 931 942 953 965 976 988

La serie E192 también se utiliza para resistencias con una tolerancia del 0.25% y 0.1% .

La coordinación modular es el nombre que se le da al sistema de valores preferentes que se utiliza en la industria de la construcción. Este sistema no se basa en series geométricas pues se ha creído que las dimensiones y los valores usados en esta área deben ser fáciles de utilizar en cálculos mentales.

Las dimensiones principales (tales como las líneas del cuadriculado en los dibujos, distancias entre el centro de las paredes, el ancho de los estantes y otros componentes de la cocina) son múltiplos de 100mm (un decímetro). Este valor es llamado módulo básico y en los estándares se representa con la letra M. Se acostumbra usar múltiplos de 300mm (3M) y 600mm (6M) del módulo básico (ver pie métrico). Para dimensiones mayores, se usan múltiplos de 12 M (1.2m), 15 M (1.5m), 30 M (3m) y 60 M (6m) del módulo básico. Para dimensiones pequeñas se utilizan incrementos sub-modulares 50 mm (1/2M) o 25 mm (1/4M). (ISO 2848, BS 6750).

Los valores escogidos de esta manera pueden dividirse fácilmente por muchos factores sin terminar en fracciones de milímetros. Por ejemplo, un múltiplo de 600mm (6M) siempre se puede dividir entre 2, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, etc. y siempre obtener un número entero de milímetros.

El tamaño de papel métrico estándar usa la raíz cuadrada de dos (√2) y números relacionados (√√√2, √√2, √2, 2, or 2√2) como factores entre dimensiones adyacentes (serie Lichtenberg, ISO 216).

En el ISO 216, el formato de referencia de la serie A es el A0, cuya superficie mide 1 m². La relación entre las longitudes de los lados vale uno frente a la raíz cuadrada de 2 (1:√2), redondeando a milímetros enteros. En consecuencia, cada formato de una serie resulta de duplicar el lado menor del formato inmediatamente inferior, o de dividir por la mitad el lado mayor del formato inmediatamente superior. De esta forma, la relación entre las superficies de dos formatos consecutivos de una serie siempre vale 2 (la superficie del A0 es el doble de la superficie del A1, el A1 el doble del A2, etcétera).^[1]​

El factor √2 también se utiliza para definir el grueso estándar de los lápices para dibujo técnico (0.13, 0.18, 0.25, 0.35, 0.50, 0.70, 1.00, 1.40, y 2.00 mm). En esta forma, siempre habrá un grosor de lápiz correcto para continuar un dibujo que haya sido aumentado o disminuido a un tamaño de papel estándar diferente.

Las potencias de dos (2^x) son frecuentemente utilizadas como números preferentes cuando se dimensionan componentes de computadores

   1    2    4    8   16   32   64  128  256  512 1024 ...

Cuando se requiere mayor precisión se puede agregar números preferentes multiplicando las potencias de dos con algún número entero pequeño e impar^[2]​

   3    6   12   24   48   96  192  384  768 1536 ...
   5   10   20   40   80  160  320  640 1280 2560 ...
   7   14   28   56  112  224  448  896 1792 3584 ...

Estos números corresponden a números binarios con una mayoría de bits no significativos, que son particularmente fáciles de sumar o restar en microprocesadores.

Los desarrolladores de programas deben tener en cuenta que el uso de las potencias de dos en la programación de una aplicación, especialmente al dimensionar arreglos, podría también tener desventajas. En particular, la eficiencia del caché de los microprocesadores se puede reducir drásticamente en aquellos procesadores donde la memoria caché no es totalmente asociativa.^{[cita requerida]}

En los gráficos por computadora, los valores de ancho y alto de las imágenes rasterizadas son normalmente múltiplos de 16, dado que muchos algoritmos de compresión de imágenes (JPEG, MPEG) dividen la imagen en bloques cuadrados de ese tamaño.

En algunos países, las leyes de protección al consumidor restringen los diferentes tamaños en los que un mismo producto se puede vender. De esta forma se hace más fácil para el consumidor comparar precios.

Un ejemplo de esta regulación es una directiva de la Unión Europea que establece el volumen de cierto líquidos pre-empacados (75/106/EEC [1]). Esta normativa establece los tamaños de las botellas de vino a 0.1, 0.25, 0.375, 0.5, 0.75, 1, 1.5, 2, 3, y 5 litros. Listas similares existen para muchos otros tipos de productos. Cuando es posible, se varían las series geométricas, incluso se desvían significativamente, con tal de acomodar tamaños tradicionales dentro de las listas. Tamaños adyacentes en las listas típicamente varían por factores de 2/3 o 3/4, incluso algunas veces por factores de 1/2, 4/5, o alguna otra fracción con dos enteros pequeños.

Mientras que algunos instrumentos, tales como el trombón y el theremín, pueden tocar una nota en cualquier frecuencia, otros instrumentos, como el piano, solo pueden tocar una serie limitada de tonos. Para la afinación de estos instrumentos se puede utilizar el popular método de Temperamento justo que selecciona tonos de la secuencia geométrica:

${\displaystyle f(i)=440{\mbox{ Hz }}\times 2^{\frac {i}{12}}}$,

otros métodos de afinación, menos frecuentes, han sido también históricamente importantes para la selección de las frecuencias de audio preferentes.

• ISO 3, Preferred numbers — Series of preferred numbers. International Organization for Standardization, 1973.
• ISO 17, Guide to the use of preferred numbers and of series of preferred numbers. 1973.
• ISO 497, Guide to the choice of series of preferred numbers and of series containing more rounded values of preferred numbers. 1973.
• ISO 2848, Building construction — Modular coordination — Principles and rules. 1984.
• ISO/TR 8389, Building construction — Modular coordination — System of preferred numbers defining multimodular sizes. International Organization for Standardization, 1984.
• IEC 60063, Preferred number series for resistors and capacitors. International Electrotechnical Commission, 1963
• 75/106/EEC [2], European Union Directive on volume of liquids. 1975.
• BS 2045, Preferred numbers. British Standards Institute, 1965.
• BS 2488, Schedule of preferred numbers for the resistance of resistors and the capacitance of capacitors for telecommunication equipment. 1966.
• ANSI Z17.1, American National Standard for Preferred Numbers. 1973

• Esta obra contiene una traducción derivada de «Preferred numbers» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.