Una red neuronal convolucional es un tipo de red neuronal artificial donde las neuronas artificiales, corresponden a campos receptivos de una manera muy similar a las neuronas en la corteza visual primaria (V1) de un cerebro biológico.^[1]​^[2]​Este tipo de red es una variación de un perceptron multicapa, sin embargo, debido a que su aplicación es realizada en matrices bidimensionales, son muy efectivas para tareas de visión artificial, como en la clasificación y segmentación de imágenes, entre otras aplicaciones.^[3]​

Los fundamentos de las redes neuronales convolucionales se basan en el Neocognitron, introducido por Kunihiko Fukushima en 1980.^[4]​ Este modelo fue más tarde mejorado por Yann LeCun et al. en 1998^[5]​ al introducir un método de aprendizaje basado en la propagación hacia atrás para poder entrenar el sistema correctamente. En el año 2012, fueron refinadas por Dan Ciresan y otros, y fueron implementadas para una unidad de procesamiento gráfico (GPU) consiguiendo así resultados impresionantes.^[6]​

El trabajo realizado por Hubel y Wiesel en 1959^[7]​ jugó un papel importante en la comprensión sobre cómo funciona la corteza visual, particularmente las células responsables de la selectividad de orientación y detección de bordes en los estímulos visuales dentro de la corteza visual primaria V1. Dos tipos de células principales fueron identificadas aquí, teniendo éstas campos receptivos alargados, con lo cual tienen una mejor respuesta a los estímulos visuales alargados como las líneas y los bordes. Estas se denominan células simples y células complejas.

Las células simples tienen regiones excitadoras e inhibitorias, ambas formando patrones elementales alargados en una dirección, posición y tamaño en particular en cada célula. Si un estímulo visual llega a la célula con la misma orientación y posición, de tal manera que ésta se alinea perfectamente con los patrones creados por las regiones excitadoras y al mismo tiempo se evita activar las regiones inhibitorias, la célula es activada y emite una señal.

Las células complejas operan de una manera similar. Como las células simples, éstas tienen una orientación particular sobre la cual son sensibles. Sin embargo, éstas no tienen sensibilidad a la posición. Por ello, un estímulo visual necesita llegar únicamente en la orientación correcta para que esta célula sea activada.

Otro punto importante sobre las células en la corteza visual es la estructura que éstas forman. A lo largo de la jerarquía de la corteza, comenzando por la región V1 de la corteza visual, luego siguiendo a las regiones V2, V4 e IT, se encuentra que la complejidad de los estímulos ideales incrementa cada vez más. Al mismo tiempo, las activaciones de las células se hacen menos sensibles a la posición y tamaño de los estímulos iniciales. Esto sucede como resultado de las células activando y propagando sus propios estímulos a otras células conectadas a esta jerarquía, principalmente gracias a la alternación entre células simples y complejas.

Las redes neuronales convolucionales consisten en múltiples capas de filtros convolucionales de una o más dimensiones. Después de cada capa, por lo general se añade una función para realizar un mapeo causal no-lineal.

Como redes de clasificación, al principio se encuentra la fase de extracción de características, compuesta de neuronas convolucionales y de reducción de muestreo. Al final de la red se encuentran neuronas de perceptron sencillas para realizar la clasificación final sobre las características extraídas. La fase de extracción de características se asemeja al proceso estimulante en las células de la corteza visual. Esta fase se compone de capas alternas de neuronas convolucionales y neuronas de reducción de muestreo. Según progresan los datos a lo largo de esta fase, se disminuye su dimensionalidad, siendo las neuronas en capas lejanas mucho menos sensibles a perturbaciones en los datos de entrada, pero al mismo tiempo siendo estas activadas por características cada vez más complejas.

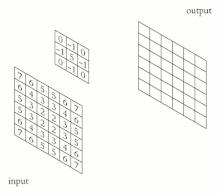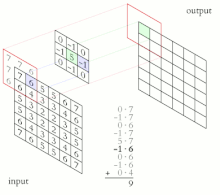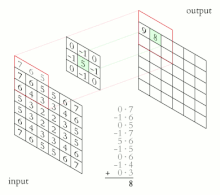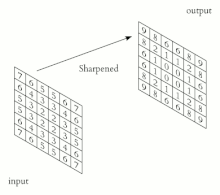
En la fase de extracción de características, las neuronas sencillas de un perceptron son reemplazadas por procesadores en matriz que realizan una operación sobre los datos de imagen 2D que pasan por ellas, en lugar de un único valor numérico. La salida de cada neurona convolucional se calcula como:

${\displaystyle Y_{j}=g\left(b_{j}+\sum _{i}K_{ij}\otimes Y_{i}\right)}$

Donde la salida ${\displaystyle Y_{j}}$ de una neurona ${\displaystyle j}$ es una matriz que se calcula por medio de la combinación lineal de las salidas ${\displaystyle Y_{i}}$ de las neuronas en la capa anterior cada una de ellas operadas con el núcleo convolucional ${\displaystyle K_{ij}}$ correspondiente a esa conexión. Esta cantidad es sumada a una influencia ${\displaystyle b_{j}}$ y luego se pasa por una función de activación ${\displaystyle g(\cdot )}$ no-lineal.

El operador de convolución tiene el efecto de filtrar la imagen de entrada con un núcleo previamente entrenado. Esto transforma los datos de tal manera que ciertas características (determinadas por la forma del núcleo) se vuelven más dominantes en la imagen de salida al tener estas un valor numérico más alto asignados a los pixeles que las representan. Estos núcleos tienen habilidades de procesamiento de imágenes específicas, como por ejemplo la detección de bordes que se puede realizar con núcleos que resaltan la gradiente en una dirección en particular. Sin embargo, los núcleos que son entrenados por una red neuronal convolucional generalmente son más complejos para poder extraer otras características más abstractas y no triviales.

Las redes neuronales cuentan con cierta tolerancia a pequeñas perturbaciones en los datos de entrada. Por ejemplo, si dos imágenes casi idénticas (diferenciadas únicamente por un traslado de algunos pixeles lateralmente) se analizan con una red neuronal, el resultado debería de ser esencialmente el mismo. Esto se obtiene, en parte, dado a la reducción de muestreo que ocurre dentro de una red neuronal convolucional. Al reducir la resolución, las mismas características corresponderán a un mayor campo de activación en la imagen de entrada.

Originalmente, las redes neuronales convolucionales utilizaban un proceso de subsampling para llevar a cabo esta operación. Sin embargo, estudio recientes han demostrado que otras operaciones, como por ejemplo max-pooling^[8]​ , son mucho más eficaces en resumir características sobre una región. Además, existe evidencia que este tipo de operación es similar a como la corteza visual puede resumir información internamente.

La operación de max-pooling encuentra el valor máximo entre una ventana de muestra y pasa este valor como resumen de características sobre esa área. Como resultado, el tamaño de los datos se reduce por un factor igual al tamaño de la ventana de muestra sobre la cual se opera.

Después de una o más fases de extracción de características, los datos finalmente llegan a la fase de clasificación. Para entonces, los datos han sido depurados hasta una serie de características únicas para la imagen de entrada, y es ahora la labor de esta última fase el poder clasificar estas características hacia una etiqueta u otra, según los objetivos de entrenamiento.

Las neuronas en esta fase funcionan de manera idéntica a las de un perceptron multicapas, donde la salida de cada una se calcula de esta forma:

${\displaystyle y_{j}=g\left(b_{j}+\sum _{i}w_{ij}\cdot y_{i}\right)}$

Donde la salida ${\displaystyle y_{j}}$ de una neurona ${\displaystyle j}$ es un valor que se calcula por medio de la combinación lineal de las salidas ${\displaystyle y_{i}}$ de las neuronas en la capa anterior cada una de ellas multiplicadas con un peso ${\displaystyle w_{ij}}$ correspondiente a esa conexión. Esta cantidad es sumada a una influencia ${\displaystyle b_{j}}$ y luego se pasa por una función de activación ${\displaystyle g(\cdot )}$ no-lineal.

Dado a la naturaleza de las convoluciones dentro de las redes neuronales convolucionales, estas son aptas para poder aprender a clasificar todo tipo de datos donde estos estén distribuidos de una forma continua a lo largo del mapa de entrada, y a su vez sean estadísticamente similares en cualquier lugar del mapa de entrada. Por esta razón, son especialmente eficaces para clasificar imágenes, por ejemplo para el auto-etiquetado de imágenes.

Sin embargo, las redes neuronales convolucionales también pueden ser aplicadas para la clasificación de series de tiempo o señales de audio utilizando convoluciones en 1D, así como para la clasificación de datos volumétricos usando convoluciones en 3D.

• U-Net
• Unidades recurrentes cerradas