Una superelipse o curva de Lamé es una figura geométrica que en coordenadas cartesianas está descrita por la siguiente ecuación:

${\displaystyle \left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1}$

donde n > 0 y a y b son los ejes de la figura.

Aunque a menudo se atribuye su invención al poeta y científico danés Piet Hein este no fue el descubridor de la superelipse. La notación cartesiana proviene del matemático francés Gabriel Lamé que generalizó la ecuación de la elipse.

Según el rango de valores de n se tienen los siguientes casos:

• n = 2 es la elipse estándar (circunferencia para a=b).
• Para n mayor que 2 se obtienen hiperelipses. En el caso límite de n infinito tenemos un rectángulo.
• Para n menor que 2 se obtienen hipoelipses.

• 
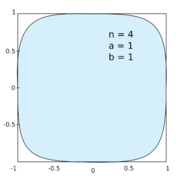
  Hiperelipse con n =4, a, b = 1.
• 
  Hipoelipse con n =3/2, a, b = 1.
• 
  Hipoelipse con n =1/2, a, b = 1.

Una expresión que sirve para aproximar a la longitud o el perímetro de una hiperelipse, es la fórmula de Rivera, en ella se utiliza el valor del "semieje mayor" (a) y el valor del "semieje menor" (b) de la hiperelipse.

Si

${\displaystyle \left\vert {\frac {x}{a}}\right\vert ^{n}+\left\vert {\frac {y}{b}}\right\vert ^{n}=1}$

Para n par, n >2, la expresión que aproxima al perímetro o longitud de una hiperelipse es:

${\displaystyle P\approx {\frac {\left({\frac {n}{2}}-1\right){\bigl (}a+b{\bigr )}+{\sqrt {a^{2}+b^{2}}}}{\frac {n}{8}}}}$

En el caso límite donde ${\displaystyle b=0}$, la fórmula da el valor exacto ${\displaystyle P=4a}$.

Las superelipses pueden ser descritas mediante las siguientes ecuaciones paramétricas:

${\displaystyle x(\theta )=\pm a\cos ^{\frac {2}{n}}(\theta )}$

${\displaystyle y(\theta )=\pm b\sin ^{\frac {2}{n}}(\theta )}$

${\displaystyle 0\leq \theta <{\frac {\pi }{2}}}$

Piet Hein fue quien popularizó el uso de la superelipse en arquitectura, diseño urbano y muebles, y el inventor del super-huevo o super-elipsoide partiendo de la superelipse:

${\displaystyle \left|{\frac {x}{4}}\right|^{2.5}\!+\left|{\frac {y}{3}}\right|^{2.5}\!=1}$

y girándola sobre el eje x. Al contrario que el elipsoide regular, el super-elipsoide es estable si se coloca sobre una superficie plana.

• Elipse
• Elipsoide
• Hipérbola
• Parábola
• Hipocicloide
• Astroide

• Weisstein, Eric W. «Superellipse». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.