La teoría de colas es el estudio matemático de las colas o líneas de espera dentro de un sistema. Esta teoría estudia factores como el tiempo de espera medio en las colas o la capacidad de trabajo del sistema sin que llegue a colapsar. Dentro de las matemáticas, la teoría de colas se engloba en la investigación de operaciones y es un complemento muy importante a la teoría de sistemas y la teoría de control. Se trata así de una teoría que encuentra aplicación en una amplia variedad de situaciones como negocios, comercio, industria, ingenierías, transporte y logística o telecomunicaciones.

La teoría de colas permite modelar sistemas en los que existe una población de agentes (también llamados clientes o usuarios) que demandan cierto servicio que es proporcionado por uno o más servidores (también llamados recursos). Dado que puede haber más agentes que recursos, pueden registrarse esperas desde que un agente llega al sistema hasta que el servidor atiende su demanda, o incluso un agente puede ser rechazado del sistema al no haber espacio donde esperar (esto es, una cola). La teoría de colas sirve para modelar procesos tales como la llegada de datos a una cola en ciencias de la computación, la congestión en red de computadoras o de telecomunicación, o la implementación de una cadena productiva en la ingeniería industrial.

En el contexto de la informática o de las tecnologías de la información y la comunicación son paradigmáticas las situaciones de espera dentro de una red de comunicaciones. Así, por ejemplo, los procesos enviados a un servidor en red forman colas de espera mientras no son atendidos; la información solicitada a un servidor Web a través de Internet puede recibirse con demora debido a la congestión en la red o en el servidor; en el caso de telefonía (fija o móvil), una llamada puede no ser realizada si alguna central está saturada (un mensaje típico en este caso es "por sobrecarga en red rogamos vuelva a llamar pasados unos minutos").

El matemático danés Agner Krarup Erlang, trabajador de la Copenhagen Telephone Exchange, publicó el primer artículo sobre la teoría de colas en 1909.^[1]​ Específicamente se preocupó del estudio del problema de dimensionamiento de líneas y centrales de conmutación telefónica para el servicio de llamadas. En su honor, la unidad de medida estadística del volumen de tráfico se denomina Erlang, así como un lenguaje de programación concurrente diseñado por Ericsson.

Cincuenta años más tarde, el científico estadounidense y pionero en el análisis de redes de ordenadores Leonard Kleinrock desarrolló el uso de herramientas de teoría de colas para en análisis de redes de conmutación de paquetes, con su tesis doctoral presentada en 1962 (y publicada en forma de libro en 1964).

Existe una población de clientes que requieren un servicio. Estos clientes entran al sistema y se unen a la cola de espera. En determinado momento se selecciona un miembro de la cola para proporcionarle el servicio mediante alguna regla (conocida como disciplina de cola). Terminado el servicio, el cliente sale del sistema de colas.

En general, la cola de espera se forma (y crece) si durante un tiempo la demanda del servicio es mayor que la capacidad del sistema para suministrarlo. Por ejemplo, si un usuario necesita un minuto para ser atendido, pero llegan dos usuarios en menos de un minuto, el segundo usuario tendrá que esperar en cola hasta ser atendido. Estos desequilibrios temporales entre demanda y capacidad suceden dado que tanto el proceso de llegadas de usuarios como el proceso de proporcionar servicio son procesos estocásticos.

En las formaciones de colas a veces se habla de clientes, tales como máquinas dañadas a la espera de ser rehabilitadas. Los clientes puede que esperen, aunque las instalaciones de servicio sean adecuadas, porque los clientes llegados anteriormente están siendo atendidos (como en el caso mencionado anteriormente). También puede suceder que los clientes esperen en cola debido a que los medios existentes sean inadecuados para satisfacer la demanda del servicio. Por ejemplo, si un usuario necesita un minuto para ser atendido pero los clientes llegan a una tasa mayor de un cliente por minuto, la cola crecerá indefinidamente.

La teoría de colas persigue caracterizar las prestaciones de un sistema compuesto por uno o más recursos que sirven a una población de clientes. En general, si un cliente llega al sistema y todos los recursos están ocupados, esperará en una cola, salvo que dicha cola esté llena y entonces será rechazado (es decir: no es admitido). La caracterización suele consistir en analizar variables tales como el tiempo medio de espera en cola, el tiempo total de estancia en el sistema o la probabilidad de ser rechazado (o admitido).

Además de esta caracterización de las prestaciones, otras aplicaciones de la teoría de colas son:

• Calcular el número de recursos necesarios para mantener la probabilidad de rechazo por debajo de un límite.
• Identificar el nivel óptimo de capacidad del sistema que minimiza un determinado coste.
• Evaluar el impacto de posibles modificaciones del sistema en sus prestaciones o rendimiento.

Se pueden identificar los siguientes elementos:

• Fuente de entrada o población potencial: Una característica de la fuente de entrada es su tamaño. El tamaño es el número total de clientes que pueden requerir servicio en determinado momento. Puede suponerse que el tamaño es infinito o finito.

• Cliente: Es todo individuo de la población potencial que solicita servicio como por ejemplo una lista de trabajo esperando para imprimirse.

• Cola: Espacio donde los clientes esperan (es decir, están haciendo cola) hasta que empiezan a ser servidos. Se caracteriza por una capacidad o tamaño máximo de la cola, que se puede suponer finita o infinita. Si es finita, es posible que se llene de clientes por lo que nuevos clientes son rechazados.

• Disciplina de la cola: mecanismo empleado para seleccionar el siguiente miembro que recibirá servicio, una vez que queda un recurso disponible. Por ejemplo, puede ser:
  • FIFO (first in first out) primero en entrar, primero en salir, según la cual se atiende primero al cliente que antes haya llegado.
  • LIFO (last in first out) también conocida como pila que consiste en atender primero al cliente que ha llegado el último.
  • RSS (random selection of service) que selecciona los clientes de manera aleatoria, de acuerdo a algún procedimiento de prioridad o a algún otro orden.
  • Processor Sharing – sirve a los clientes igualmente. La capacidad de la red se comparte entre los clientes y todos experimentan con eficacia el mismo retraso.

• Recursos o servidores: elementos encargados de proporcionar el servicio a los clientes. Se caracterizan por un proceso de servicio que típicamente define el tiempo necesario para atender un cliente (por ejemplo, si es un tiempo aleatorio, la variable aleatoria que lo caracteriza).

• Redes de colas: Sistema donde existen varias colas y los trabajos fluyen de una a otra. Por ejemplo: las redes de comunicaciones o los sistemas operativos multitarea.

David G. Kendall introdujo una notación de colas A/S/c en 1953^[2]​ en la que A describe la distribución del tiempo entre llegada, S la distribución del tiempo de servicio y c el número de recursos disponibles. Ha sido desde entonces extendida a A/S/c/K/N/D^[3]​^[4]​ donde K es la capacidad total de la cola (es decir, el número máximo de usuarios en el sistema en cualquier momento), N el número de usuarios que generan peticiones, y D es la disciplina de cola.

Para describir la distribución de los tiempos entre llegadas A o de servicio S se suele emplear alguno de estos valores:

• M para "Markoviano" o "sin memoria", lo que implica que los tiempos entre llegadas siguen una distribución exponencial (por lo tanto, el número de llegadas en un intervalo de tiempo sigue una distribución de Poisson).
• D para unos tiempos entre llegadas deterministas, es decir, que no siguen un proceso aleatorio. .
• G para una "distribución general" de los tiempos entre llegadas.

Mientras que para la disciplina de cola D se suele emplear alguno de estos valores:

• First Come First Served (FCFS) o First In First Out (FIFO)
• Last Come First Served (LCFS) o Last In First Out (LIFO)
• Service In Random Order (SIRO)
• Processor Sharing

La capacidad del sistema K puede tomar un valor finito determinado o infinito. Si es finito, el número máximo de clientes permitidos en el sistema está acotado, por lo que nuevas llegadas son rechazadas. Si es infinito, no se produce rechazo.

Si el tamaño de la población N es finito, esto supone que cuantos más usuarios se encuentren en el sistema, menos usuarios estarán generando peticiones. Si por el contrario el tamaño N es infinito, la tasa de generación de peticiones se mantendrá constante independientemente del número de usuarios en el sistema.

Los tres primeros parámetros de la notación de Kendall siempre se indican de forma explícita, mientras que si los otros tres no aparecen es porque se suponen unos valores por defecto. Dichos valores son:^[5]​

• Para la capacidad K, se supone infinita.
• Para la disciplina de cola D, se supone FCFS.
• Para la población D, se supone infinita.

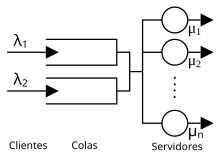
• M/M/1/ (∞/FIFO/∞): Se trata de una de las colas más sencillas. Las llegadas siguen un proceso de Poisson, las peticiones tienen un tiempo de servicio que sigue una variable aleatoria exponencial y únicamente hay un servidor. No se suelen especificar los parámetros K, N y D, lo que supone los siguientes valores por defecto: la capacidad del sistema es infinita, la prioridad es FCFS, y la población que genera las peticiones es infinita (lo que implica que la tasa de llegadas es constante). Esta cola se ilustra en el primer sistema de la figura.
• M/M/n/n: No hay cola de espera, sino n recursos (servidores) y hasta n usuarios como máximo; si llega el usuario n+1, es rechazado. Este modelo suele aplicarse para analizar las prestaciones en telefonía convencional. La probabilidad de que un usuario sea rechazado se calcula con la fórmula Erlang-B. También suele identificarse como M/M/c/c o M/M/k/k.
• M/M/c: La capacidad del sistema es ilimitada, aunque haya sólo n recursos; en caso de llegar el usuario n+1, éste no será rechazado sino que pasará a una cola de espera. Este modelo puede aplicarse para analizar un call center en el que un número fijo de operadores resuelven peticiones, que pueden quedar en espera hasta ser atendidas. La probabilidad de que un usuario no sea atendido directamente sino que tenga que esperar se calcula con la fórmula Erlang-C. Esta cola se ilustra para el caso de M/M/3 en el segundo sistema de la figura. También se identifica como M/M/k o M/M/n.

La notación de Kendall no sirve para representar redes de colas, como es el caso de los dos últimos sistemas de la figura:

• Colas en paralelo: el tercer sistema de la figura, en el que el proceso de llegada se divide en varias colas, típicamente independientes. Se podría corresponder con una estación de servicio donde cada servidor tiene una cola independiente y los usuarios no se mueven entre colas.
• Colas en serie (o sistema en tándem): el cuarto sistema de la figura. El proceso de salida del primer sistema supone el proceso de entrada para el segundo sistema. Se podría corresponder con tareas en un ordenador que deben ejecutarse en diferentes procesadores.

Las medidas de rendimiento (o desempeño) de interés dependen del escenario de aplicación. Por ejemplo, en el caso de un servidor de peticiones web, suele ser interesante el tiempo total que tarda una petición en ser atendida, mientras que para diseñar un centro de atención al cliente (call center), una medida fundamental sería el tiempo que espera un cliente hasta que es atendido, dado que su tiempo de atención es menos importante. Aun así, existe un conjunto de medidas de rendimiento que suelen ser comunes a todos los sistemas:

• T: tiempo medio de estancia en el sistema, definido como el tiempo que transcurre desde que una petición llega al sistema (es generada por la población) hasta que ha sido finalmente atendida por un recurso (abandona el sistema).

• W: tiempo medio de estancia en la cola, definido como es el tiempo desde que una petición llega al sistema hasta que empieza a ser atendida por uno de los recursos.

Ambos tiempos se relacionan a través del tiempo medio de servicio S mediante la expresión T = W + S

• N: número medio de usuarios en el sistema, media temporal del número de usuarios (o peticiones) que se encuentran en el sistema, ya sea en la cola o siendo atendidos por algún recurso.

• Q: número medio de usuarios en la cola, definido como la media del número de usuarios esperando a ser atendido.

• ρ: factor de utilización u ocupación de los recursos, definido como la proporción de tiempo que un usuario está atendiendo a usuarios (es decir, no está desocupado).

Dado un sistema con c recursos, estas variables están relacionadas mediante la expresión N = Q + c ρ

Se trata de un resultado fundamental que establece una relación muy sencilla entre dos medidas de rendimiento: el número medio de usuarios N y el tiempo medio de estancia en el sistema T. Dada una tasa efectiva de entrada al sistema ${\displaystyle \lambda }$ (esto es, teniendo en cuenta únicamente los usuarios que son atendidos, y no los que son rechazados), la relación viene dada por

${\displaystyle N=\lambda T}$

Existe una "demostración gráfica"^[6]​ del teorema, donde resulta destacable las pocas hipótesis de modelado necesarias (esto es: no es necesario suponer llegadas de Poisson, tiempos de servicio exponenciales, etc.).

En este modelo, según la notación de Kendall, la tasa de llegadas ${\displaystyle \lambda }$ y la tasa de servicio ${\displaystyle \mu }$ siguen una distribución de Poisson, sólo hay un servidor y la capacidad del sistema es ilimitada. Si la tasa de llegadas fuese mayor que la tasa de servicio (${\displaystyle \lambda >\mu }$), dado que el sistema tiene una capacidad infinita, el número de usuarios crecería indefinidamente y no podría calcularse medidas de rendimiento.^[7]​

En caso de que ${\displaystyle \lambda <\mu }$, la ocupación del recurso puede calcularse como:

${\displaystyle \rho ={\frac {\lambda }{\mu }}}$

Por lo tanto, únicamente puede analizarse el sistema si ${\displaystyle \rho <1}$. En este caso, el número medio de usuarios en el sistema se puede obtener analizando el proceso de nacimiento y muerte resultante, y viene dado por:

${\displaystyle N={\frac {\rho }{1-\rho }}}$

Aplicando el teorema de Little, el tiempo medio de estancia en el sistema viene dado por:

${\displaystyle T={\frac {1/\mu }{1-\rho }}={\frac {1}{\mu -\lambda }}}$

El tiempo medio de estancia en la cola viene dado por:

${\displaystyle W=T-{\frac {1}{\mu }}={\frac {\rho /\mu }{1-\rho }}}$

Mientras que el número medio de usuarios en la cola viene dado por la expresión:

${\displaystyle Q=\lambda W={\frac {\rho ^{2}}{1-\rho }}}$

En este modelo, al igual que en caso anterior, la tasa de llegadas ${\displaystyle \lambda }$ y la tasa de servicio ${\displaystyle \mu }$ siguen una distribución de Poisson, y hay un espacio infinito para esperar. Sin embargo, ahora existen c (un número entero positivo) servidores idénticos en paralelo, y cualquiera de ellos puede atender las peticiones en cuando estén disponibles. La ocupación del sistema, o de cualquiera de los servidores, puede calcularse como^[8]​

${\displaystyle \rho ={\frac {\lambda }{c\mu }}}$

Y al igual que en el caso del M/M/1, únicamente puede analizarse el sistema si ${\displaystyle \rho <1}$. También se define una variable ${\displaystyle I}$ que representa una "intensidad" de tráfico, que viene dada por la expresión:

${\displaystyle I={\frac {\lambda }{\mu }}}$,

y que vendría a representar el número mínimo de servidores necesarios para atender la carga en el sistema. ${\displaystyle I}$ estrictamente no tiene unidades pero se mide en "Erlangs". La probabilidad de tener que esperar a ser atendido (una de las variables de rendimiento más importantes) viene dada por la expresión conocida como "Erlang-C"

${\displaystyle P_{Q}=E_{c}(m,I)={\frac {\frac {I^{m}}{m!}}{(1-\rho )\left(\sum _{n=0}^{m-1}{\frac {I^{n}}{n!}}\right)+{\frac {I^{m}}{m!}}}}}$

Para el cálculo del resto de variables de desempeño, resulta conveniente en primer lugar calcular la probabilidad de que el sistema esté vacío mediante la expresión:

${\displaystyle p_{0}=\left(\left(\sum _{n=0}^{m-1}{\frac {I^{n}}{n!}}\right)+{\frac {I^{m}}{m!}}\cdot {\frac {1}{1-\rho }}\right)^{-1}.}$

A partir de esta probabilidad, se puede calcular el número medio de usuarios en cola

${\displaystyle Q={\frac {I^{m}}{m!}}{\frac {\rho }{(1-\rho )^{2}}}p_{0}}$

Una vez obtenido Q, el tiempo medio de espera en cola se puede obtener gracias al teorema de Little como ${\displaystyle W=Q/\lambda }$, y el tiempo medio de estancia en el sistema como ${\displaystyle T=W+1/\mu }$

De nuevo, tanto la tasa de llegadas ${\displaystyle \lambda }$ como la tasa de servicio ${\displaystyle \mu }$ siguen una distribución de Poisson, y existen c servidores idénticos en paralelo. Sin embargo, en este sistema la capacidad (es decir, el número máximo de usuarios) también es c, por lo que no existe una cola de espera, de lo que se deduce directamente que

${\displaystyle Q=W=0}$

por lo que el tiempo medio total es el tiempo medio de servicio

${\displaystyle T={\frac {1}{\mu }}}$

Dado que no hay cola de espera, cuando un usuario llega al sistema sólo caben dos opciones: si queda algún servidor disponible el usuario es inmediatamente atendido, mientras que si todos los c servidores están ocupado el usuario es rechazado.

La probabilidad de que un usuario llegue al sistema y sea rechazado se puede analizar con un proceso de nacimiento y muerte de c+1 estados (desde 0 hasta c), con tasas de transición similares al sistema M/M/1. Dicha probabilidad es la variable de rendimiento más importante y su expresión se conoce como Erlang-B:

${\displaystyle P_{B}=E_{b}(c,I)={\frac {\frac {I^{c}}{c!}}{\sum \limits _{n=0}^{c}{\frac {I^{n}}{n!}}}}}$

La teoría de formación de una cola es a menudo demasiado restrictiva matemáticamente para ser capaz de modelar todas las situaciones verdaderas a nivel mundial. Por ejemplo; los modelos matemáticos a menudo asumen el número de clientes, o la capacidad de la cola infinitos, cuando es evidente que deben estar limitados. Los medios alternativos del análisis de la teoría de colas consisten generalmente en simulaciones de ordenador o en el análisis de datos experimentales.

Las redes telefónicas se diseñan para acomodar la intensidad ofrecida del tráfico con solamente una pequeña pérdida. El funcionamiento de los sistemas depende de si la llamada es rechazada, de si está perdida, etc. Normalmente los sistemas de desbordamiento hacen uso de rutas alternativas e incluso estos sistemas tienen una capacidad de carga finita o máxima de tráfico. Sin embargo, el uso de las colas permite que los sistemas esperen por las peticiones de su cliente hasta que los recursos libres estén disponibles. Esto significa que si los niveles de la intensidad del tráfico exceden de la capacidad disponible, las llamadas del cliente se perderían. La disciplina de colas determina la manera de cómo manejar las llamadas de los clientes. Define la manera en que les servirán, la orden de las cuales se sirven, y la manera en la que los recursos se dividen entre los clientes.

En particular, el supuesto de tiempos entre llegadas exponenciales implica que las llegadas ocurren al azar (proceso de entrada de Poisson), lo cual es una aproximación razonable en muchas situaciones pero no cuando las llegadas están programadas o reguladas con todo cuidado. Todavía más, las distribuciones de tiempos de servicio reales con frecuencia se desvían bastante de la forma exponencial, en particular cuando los requerimientos de servicio de los clientes son muy parecidos. Por ello, es importante disponer de otros modelos de colas que usen otras distribuciones de probabilidad. Desafortunadamente, el análisis matemático de los modelos de colas con distribuciones no exponenciales es mucho más difícil. Sin embargo, se han podido obtener algunos resultados útiles con algunos modelos.^[9]​

• Unidad Erlang
• Ingeniería industrial
• Distribución de Poisson
• Throughput
• Planificador
• Congestión vehicular
• Red de flujo
• Distribución de Erlang
• Distribución Exponencial
• Cola (estructura de datos)
• Cola de prioridad (estructura de datos)
• Congestión de red

• A. Blasco, S. Pérez-Díaz, Modelos aleatorios en Ingeniería - Editorial Paraninfo - ISBN13: 9788428337236 (Capítulo 6, Introducción a la Teoría de colas)
• Gross, Donald; Carl M. Harris (1998). Fundamentals of Queueing Theory. Wiley. ISBN 0-471-32812-X.  Online
• Deitel, Harvey M. (1984) [1982]. An introduction to operating systems (revisited first edición). Addison-Wesley. p. 673. ISBN 0-201-14502-2.  chap.15, pp. 380–412
• Lazowska, Edward D.; John Zahorjan; G. Scott Graham; Kenneth C. Sevcik (1984). Quantitative System Performance: Computer System Analysis Using Queueing Network Models. Prentice-Hall, Inc. ISBN 0-13-746975-6. 
• Serrano, Pablo; Hernández, José A. (2024). Una introducción amable a la teoría de colas. Universidad Carlos III de Madrid. 
• Zukerman, Moshe. Introduction to Queueing Theory and Stochastic Teletraffic Models. 

• Artículos de Teoría de Colas
• Queueing Theory Basics
• Calculadora de Teoría de Colas