La alternación de un cubo genera un tetraedro

La alternación de un cuboctaedro truncado genera un cubo romo (no uniforme)

En geometría, una alternación o truncamiento parcial es una operación en un polígono, poliedro, teselado o politopo de dimensiones superiores, que elimina vértices alternativamente.^[1]​

Coxeter designa la alternación utilizando una letra h como prefijo, que significa hemi o mitad. Debido a que la alternancia reduce todas las caras del polígono a la mitad de aristas, solo se puede aplicar a politopos tales que todas sus caras tienen un número de lados par. Una cara cuadrada alternada se convierte en un dígono, y al estar degenerada, suele reducirse a una sola arista.

De manera más general, cualquier poliedro o mosaico vértices-uniforme con una configuración de vértices en la que todos sus elementos tienen números de vértices pares, se puede alternar. Por ejemplo, la alternación de una figura de vértice con 2a.2b.2c es a.3.b.3.c.3, donde el tres es el número de elementos en esta figura de vértice. Un caso especial son las caras cuadradas, cuyo orden se divide por la mitad para originar dígonos degenerados. Así, por ejemplo, el cubo 4.4.4 se alterna como 2.3.2.3.2.3 que se reduce a 3.3.3, siendo el tetraedro; y las 6 aristas del tetraedro también se pueden ver como las caras degeneradas del cubo original.

Un achatado (snub en la terminología de Coxeter) puede verse como una alternanción de un poliedro regular truncado o de un poliedro cuasiregular truncado. En general, un poliedro puede ser achatado si su truncamiento solo tiene caras con números de vértices pares. Todos los poliedros truncados rectificados incumplen este criterio, al igual que los poliedros regulares.

El antiprisma cuadrado romo es un ejemplo de achatado general, y se puede representar mediante ss{2,4}, siendo el antiprisma cuadrado, s{2,4}.

Esta operación de alternación se aplica también a politopos y panales de dimensiones superiores, pero en general la mayoría de los resultados de esta operación no serán uniformes. Los vacíos creados por los vértices eliminados en general no crearán facetas uniformes y, también con carácter general tampoco se dispone de suficientes grados de libertad para permitir un cambio de escala apropiado de las nuevas aristas. Sin embargo, existen excepciones, como la generación del 24-celdas romo a partir del 24-celdas truncado.

Ejemplos:

• Panales
  1. Un panal cúbico alternado es el panal tetraédrico-octaédrico.
  2. Un panal prismático hexagonal alternado es el panal cúbico alternado girado.
• Polícoro
  1. Un 24-celdas truncado alternado es el 24-celdas romo.
• 4-panales:
  1. Un panal 24-celdas truncado alternado es el panal 24-celdas romo.
• Un hipercubo siempre se puede alternar en un demihipercubo uniforme.
  1. Cubo → Tetraedro (regular)
     • →
  2. Teseracto (8-celdas) → 16-celdas (regular)
     • →
  3. Penteracto → demipenteracto (semiregular)
  4. Hexeracto → demihexeracto (uniforme)
  5. ...

Coxeter también utilizó el operador a, que contiene ambas mitades, por lo que conserva la simetría original. Para poliedros regulares de lados pares, a{2p,q} representa un politopo compuesto con dos copias opuestas de h{2p,q}. Para poliedros regulares de lados impares, mayores que 3, a{p,q}, se convierte en un poliedro estrellado.

Norman Johnson amplió el uso del operador alterado a{p,q}, b{p,q} para el sólido combinado; y c{p,q} para el convertido, como , y respectivamente.

El poliedro compuesto conocido como estrella octángula se puede representar mediante a{4,3} (un cubo alterado) y , .

El poliedro estrellado conocido como pequeño icosidodecaedro ditrigonal se puede representar mediante a{5,3} (un dodecaedro alterado) y , . Aquí todos los pentágonos se han alternado en pentagramas y se han insertado triángulos para ocupar las aristas libres resultantes.

El poliedro estrellado conocido como gran icosidodecaedro ditrigonal se puede representar mediante a{5/2,3} (un gran dodecaedro estrellado alterado) y , . Aquí todos los pentagramas se han alternado nuevamente en pentágonos y se han insertado triángulos para ocupar las aristas libres resultantes.

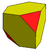
Una operación similar consiste en truncar vértices alternadamente, en lugar de simplemente eliminarlos. A continuación se muestra un conjunto de poliedros que se pueden generar a partir de los sólidos de Catalan. Estos tienen dos tipos de vértices que pueden truncarse alternativamente. Truncar los vértices de orden superior y ambos tipos de vértices produce las formas siguientes:

Nombre	Original	Truncamiento alternado	Truncamiento	Nombre del truncado
Cubo Dual del tetraedro rectificado				Cubo truncado alternado
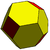
Rombododecaedro Dual del cuboctaedro				Dodecaedro rómbico truncado
Triacontaedro rómbico Dual del icosidodecaedro				Triacontaedro rómbico truncado
Triaquistetraedro Dual del tetraedro truncado				Triaquistetraedro truncado
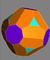
Triaquisoctaedro Dual del cubo truncado				Triaquisoctaedro truncado
Triaquisicosaedro Dual del dodecaedro truncado				Triaquisicosaedro truncado

• Portal:Matemática. Contenido relacionado con Matemática.
• Portal:Geometría. Contenido relacionado con Geometría.
• Notación de poliedros de Conway
• Construcción de Wythoff

• Coxeter, H.S.M. Regular Polytopes, (3.ª edición, 1973), edición de Dover, ISBN 0-486-61480-8
• Norman Johnson Politopos uniformes, Manuscrito (1991)
  • N.W. Johnson: La teoría de los politopos uniformes y los panales, Ph.D. Disertación, Universidad de Toronto, 1966
• Weisstein, Eric W. «Snubification». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Richard Klitzing, Desaires, facetas alternadas y diagramas de Stott-Coxeter-Dynkin, Simetría: cultura y ciencia, vol. 21, n.º 4, 329-344, (2010) [1]

• Olshevsky, George. "Alternation". Glossary for Hyperspace. Archived from the original on 4 February 2007
• Nombres de poliedros, desaire

Operadores de poliedros

Semilla	Truncamiento	Rectificación	Bitruncamiento	Dual	Expansión	Omnitruncamiento	Alternaciones
t0{p,q} {p,q}	t01{p,q} t{p,q}	t1{p,q} r{p,q}	t12{p,q} 2t{p,q}	t2{p,q} 2r{p,q}	t02{p,q} rr{p,q}	t012{p,q} tr{p,q}	ht0{p,q} h{q,p}	ht12{p,q} s{q,p}	ht012{p,q} sr{p,q}