
En teoría de categorías, un funtor o functor es una función de una categoría a otra que hace corresponder objetos con objetos y morfismos con morfismos, de manera que la composición de morfismos y las identidades se preservan.
Los funtores se consideraron primero en topología algebraica, donde se asocian los objetos algebraicos con los espacios topológicos y se asocian los homomorfismos algebraicos con las funciones continuas. Hoy en día, los funtores se utilizan a través de las matemáticas modernas para relacionar varias categorías.
Ejemplos de functores típicos son el funtor fiel y el funtor pleno.
Definición
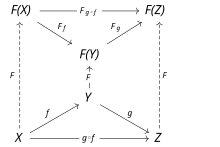
Sean C y D dos categorías. Un funtor F de C a D es una correspondencia que[1]
- Asocia a cada objeto en C a un objeto en D,
- Asocia cada morfismo en C a un morfismo en D de tal manera que las siguientes dos condiciones se mantienen:
- para todo objeto en C,
- para todos los morfismos y en C.
Es decir, los funtores deben conservar los morfismos de identidad y la composición de morfismos.
Covarianza y contravarianza
Existen muchas construcciones en matemáticas que serían funtores si no fuera por el hecho de que "invierten los morfismos" e "invierten la composición". En consecuencia, se define un funtor contravariante F de C a D como una aplicación que
- Asocia cada objeto en C con un objeto en D,
- Asocia cada morfismo en C con un morfismo en D tal que se cumplan las dos condiciones siguientes:
- para cada objeto en C,
- para todos los morfismos y en C.
Debe tenerse en cuenta que los funtores contravariantes invierten la dirección de la composición.
Los funtores ordinarios también se denominan funtores covariantes para distinguirlos de los contravariantes. Tenga en cuenta que también se puede definir un funtor contravariante como un funtor covariante en la categoría opuesta .[2] Algunos autores prefieren escribir todas las expresiones de manera covariante. Es decir, en lugar de decir que es un funtor contravariante, simplemente escriben (o, a veces, ) y lo llaman funtor.
Los funtores contravariantes también se denominan ocasionalmente cofuntores.[3]
Existe una convención que se refiere a vectores, es decir, a campos vectoriales, elementos del espacio de secciones de un fibrado tangente , como contravariantes y a covectores, es decir, 1-formas, elementos del espacio de secciones de un fibrado cotangente —como covariante. Esta terminología se origina en la física, y su fundamento tiene que ver con la posición de los índices (arriba y abajo) en expresiones como para o para En este formalismo se observa que el símbolo de transformación de coordenadas (que representa la matriz ) actúa sobre las coordenadas covectoriales de la misma manera que sobre los vectores base: , mientras que actúa de manera opuesta sobre las coordenadas vectoriales (pero de la misma manera como en los covectores base: ). Esta terminología es contraria a la utilizada en la teoría de categorías porque son los covectores los que tienen retrocesos en general y, por tanto, son contravariantes, mientras que los vectores en general son covariantes ya que pueden ser puestos hacia adelante. Véase también covarianza y contravarianza.
Funtor opuesto
Cada funtor induce el funtor opuesto , donde y son las categorías opuestas de y .[4] Por definición, asigna objetos y morfismos de la misma manera que . Dado que no coincide con como categoría, y de manera similar para , se distingue de . Por ejemplo, al componer con , se debe usar o . Téngase en cuenta que, siguiendo la propiedad de categoría opuesta, .
Bifuntores y multifuntores
Un bifuntor (también conocido como funtor binario) es un funtor cuyo dominio es una categoría producto. Por ejemplo, el homomorfismo funtorial es del tipo Cop × C → Set. Puede verse como un funtor con dos argumentos. El homomorfismo funtorial es un ejemplo natural; es contravariante en un argumento y covariante en el otro.
Un multifuntor es una generalización del concepto de funtor a n variables. Entonces, por ejemplo, un bifuntor es un multifuntor con n= 2.
Propiedades
Dos consecuencias importantes de la axiomática de los funtores son:
- F transforma cada diagrama conmutativo en C en un diagrama conmutativo en D
- Si f es un isomorfismo en C, entonces F(f) es un isomorfismo en D
Se pueden componer funtores, es decir, si F es un funtor de A a B y G es un funtor de B a C, entonces se puede formar el funtor compuesto G ∘ F de A a C. La composición de los funtores es asociativa donde se define. La identidad de la composición de funtores es el funtor identidad. Esto muestra que los funtores pueden considerarse como morfismos en categorías de categorías, por ejemplo en la categoría de categorías pequeñas.
Una categoría pequeña con un solo objeto es lo mismo que un monoide: los morfismos de una categoría de un solo objeto pueden considerarse elementos del monoide, y la composición en la categoría se considera la operación monoide. Los funtores entre categorías de un solo objeto corresponden a homomorfismos monoides. Entonces, en cierto sentido, los funtores entre categorías arbitrarias son una especie de generalización de los homomorfismos monoides a categorías con más de un objeto.
Ejemplos
- Diagrama
- Para las categorías C y J, un diagrama de tipo J en C es un funtor covariante .
- Prehaz (teoría de categorías)
- Para las categorías C y J, un prehaz J en C es un funtor contravariante . En el caso especial en el que J es un conjunto, la categoría de conjuntos y funciones, D se denomina prehaz en C.
- Prehaces (sobre un espacio topológico)
- Si X es un espacio topológico, entonces los conjunto abiertos en X forman un conjunto parcialmente ordenado abierto (X) bajo inclusión. Como todo conjunto parcialmente ordenado, abierto (X) forma una pequeña categoría añadiendo una sola flecha U → V si y solo si . Los funtores contravariantes en abierto (X) se denominan prehaces en X. Por ejemplo, asignando a cada conjunto abierto U el álgebra asociativa de funciones continuas con valores reales en U, se obtiene un prehaz de álgebras en X.
- Funtor constante
- El funtor C → D que asigna cada objeto de C a un objeto fijo X en D y cada morfismo en C al morfismo de identidad en X. Este tipo de funtor se denomina funtor constante o de selección.
- Endofuntor
- Un funtor que asigna una categoría a esa misma categoría; por ejemplo, el funtor polinómico.
- Funtor identidad
- En la categoría C, escrita 1C o idC, asigna un objeto a sí mismo y un morfismo a sí mismo. El funtor de identidad es un endofuntor.
- Funtor diagonal
- El funtor diagonal se define como el funtor de D a la categoría de funtor DC que envía cada objeto en D al funtor constante en ese objeto.
- Funtor límite
- Para una categoría de índices J fija, si cada funtor J → C tiene un límite (por ejemplo, si C está completo), entonces el funtor límite CJ → C asigna a cada funtor su límite. La existencia de este funtor se puede probar al darse cuenta de que es el adjunto por la derecha del funtor diagonal e invocar los funtores adjuntos. Esto requiere una versión adecuada del axioma de elección. Se aplican observaciones similares al funtor colímite (que asigna a cada funtor su colímite y es covariante).
- Funtor de conjuntos de potencias
- El funtor de conjuntos de potencias P : Set → Set asigna cada conjunto a su conjunto potencia y cada función a la aplicación que envía a su imagen . También se puede considerar el funtor de conjunto de potencias contravariante que hace corresponder a la aplicación que hace corresponder a su imagen . Por ejemplo, si entonces . Supóngase que y . Entonces, es la función que envía cualquier subconjunto de a su imagen , que en este caso significa , donde denota la aplicación bajo , por lo que también podría escribirse como . Para los demás valores, Téngase en cuenta que genera en consecuencia una topología trivial en . También debe tenerse en cuenta que, aunque la función en este ejemplo se asigna al conjunto de potencias de , ese no tiene por qué ser el caso en general.
- Espacio vectorial dual
- La aplicación que asigna a cada espacio vectorial su espacio dual y a cada aplicación lineal su dual o transpuesta es un funtor contravariante de la categoría de todos los espacios vectoriales sobre un cuerpo fijo sobre sí mismo.
- Grupo fundamental
- Considérese la categoría de los espacios topológicos puntados, es decir, espacios topológicos con puntos diferenciados. Los objetos son pares (X, x0), donde X es un espacio topológico y x0 es un punto en X. Un morfismo de (X, x0) a (Y, y0) viene dado por una aplicación continua f : X → Y con f(x0)= y0. Para cada espacio topológico X con un punto diferenciado x0, se puede definir el grupo fundamental basado en x0, denotado como π1(X, x0). Este es el grupo de las clases de bucles homotópicos basados en x0, con la operación grupal de concatenación. Si f : X → Y es un morfismo de espacios topológicos puntados, entonces cada bucle en X con punto base x, 0 se puede componer con f para producir un bucle en Y con punto base y0. Esta operación es compatible con la relación de equivalencia homotópica y la composición de bucles, y se obtiene un homomorfismo de grupos de π(X, x0) a π(Y, y0). Se obtiene así un funtor de la categoría de espacios topológicos puntuados a la categoría de grupos. En la categoría de espacios topológicos (sin puntos diferenciados), se consideran clases de homotopía de curvas genéricas, pero no se pueden componer a menos que compartan un punto final. Así se tiene el grupoide fundamental en lugar del grupo fundamental, y esta construcción es funtorial.
- Álgebra de funciones continuas
- Un funtor contravariante de la categoría de espacios topológicos (con aplicaciones continuas como morfismos) a la categoría de álgebras asociativas reales se obtiene asignando a cada espacio topológico X el álgebra C(X) de todas las funciones continuas de valor real en ese espacio. Toda aplicación continua f : X → Y induce un álgebra sobre un cuerpo C(f) : C(Y) → C(X) mediante la regla C(f)(φ)= φ ∘ f para cada φ en C(Y).
- Haces tangentes y cotangentes
- La aplicación que envía cada variedad diferenciable a su fibrado tangente y cada función infinitamente diferenciable a su derivada es un funtor covariante de la categoría de variedades diferenciables a la categoría de los fibrados vectoriales. Al hacer estas construcciones puntuales se obtiene el espacio tangente, un funtor covariante de la categoría de variedades diferenciables puntuadas sobre la categoría de espacios vectoriales reales. Asimismo, un espacio cotangente es un funtor contravariante, esencialmente la composición del espacio tangente con el espacio dual anterior.
- Acciones/representaciones grupales
- Cada grupo G puede considerarse como una categoría con un solo objeto cuyos morfismos son los elementos de G. Un funtor de G a Set no es más que una acción de grupo de G en un conjunto particular, es decir, un conjunto G. Asimismo, un funtor de G sobre una categoría de espacios vectoriales, VectK, es una representación de G. En general, un funtor G → C puede considerarse como una acción de G sobre un objeto de la categoría C. Si C es un grupo, entonces esta acción es un homomorfismo de grupo.
- Álgebras de Lie
- Asignar a cada grupo de Lie real (complejo) su álgebra de Lie real (compleja) define un funtor.
- Productos tensoriales
- Si C denota la categoría de espacios vectoriales sobre un campo fijo, con aplicaciones lineales como morfismos, entonces el producto tensorial define un funtor C × C → C que es covariante en ambos argumentos.[5]
- Funtores olvidadizos
- el funtor U : Grp → Set que asigna un grupo a su conjunto subyacente y un homomorfismo de grupos a su función subyacente de conjuntos es un funtor.[6] Funtores como estos, que olvidan alguna estructura, se denominan funtor olvidadizo. Otro ejemplo es el funtor Rng → Ab que asigna un anillo a su grupo abeliano aditivo subyacente. Los morfismos en Rng (homomorfismos de anillos) se convierten en morfismos en Ab (homomorfismos de grupo abeliano).
- Funtores libres
- Los funtores libres van en la dirección opuesta a los funtores olvidadizos. El funtor libre F : Set → Grp envía cada conjunto X al grupo libre generado por X. Las funciones se asignan a homomorfismos de grupo entre grupos libres. Existen construcciones libres para muchas categorías basadas en conjuntos estructurados (véase objeto libre).
- Grupos de homomorfismo
- A cada par A, B de grupos abelianos se le puede asignar el grupo abeliano Hom(A, B) que consta de todos los homomorfismos de grupos desde A hasta B. Este es un funtor que es contravariante en el primer argumento y covariante en el segundo argumento, es decir, es un funtor Abop × Ab → Ab (donde Ab denota la categoría de grupos abelianos con homomorfismos de grupo). Si f : A1 → A2 y g : B1 → B2 son morfismos en Ab, entonces el homomorfismo de grupo Hom(f, g): Hom(A2, B1) → Hom(A1, B2) viene dado por φ ↦ g ∘ φ ∘ f (véase funtor homomorfo.
- Funtores representables
- Se puede generalizar el ejemplo anterior a cualquier categoría C. A cada par X, Y de objetos en C se le puede asignar el conjunto Hom(X, Y) de morfismos de X sobre Y. Esto define un funtor para Set que es contravariante en el primer argumento y covariante en el segundo, es decir, es un funtor Cop × C → Set. Si f : X1 → X2 y g : Y1 → Y2 son morfismos en C, entonces la aplicación Hom(f, g) : Hom(X2, Y1) → Hom(X1, Y2) viene dada por φ ↦ g ∘ φ ∘ f. Funtores como estos se denominan representables. Un objetivo importante en muchos entornos es determinar si un funtor determinado es representable.
Véase también
Referencias
- ↑ Jacobson, 2009, p. 19, def. 1.2.
- ↑ Jacobson, 2009, pp. 19–20.
- ↑ Popescu, Nicolae; Popescu, Liliana (1979). Theory of categories. Dordrecht: Springer. p. 12. ISBN 9789400995505. Consultado el 23 de abril de 2016.
- ↑ Mac Lane, Saunders; Moerdijk, Ieke (1992), Sheaves in geometry and logic: a first introduction to topos theory, Springer, ISBN 978-0-387-97710-2.
- ↑ Hazewinkel, Michiel; Gubareni, Nadezhda Mikhaĭlovna; Gubareni, Nadiya; Kirichenko, Vladimir V. (2004), Algebras, rings and modules, Springer, ISBN 978-1-4020-2690-4.
- ↑ Jacobson, 2009, p. 20, ex. 2.
Bibliografía
- Jacobson, Nathan (2009), Basic algebra 2 (2nd edición), Dover, ISBN 978-0-486-47187-7.





































































