
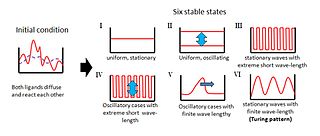


El concepto de patrón de Turing (a menudo referido en plural como patrones de Turing) fue introducido por el matemático inglés Alan Turing en 1952 en su artículo titulado La Base Química de la Morfogénesis.[1] Este artículo fundacional describe la manera en que los patrones en la naturaleza como rayas y puntos pueden surgir naturalmente a partir de un estado uniforme homogéneo.
Visión general
[editar]La teoría original, la teoría de reacción-difusión de la morfogénesis, ha sido útil como un modelo importante en la biología teórica.[2] Los sistemas de reacción–difusión han atraído mucho interés como modelos prototipo para la formación de patrones. Patrones como frentes, hexágonos, espirales, rayas y solitones disipativos fueron encontrados en varios tipos de sistemas de reacción-difusión, a pesar de grandes discrepancias, en los términos de reacción. Es una teoría importante en biología del desarrollo; por ejemplo, hubo un estudio teórico sobre el potencial VEGF para formar patrones de Turing para regular la linfangiogénesis en el embrión del danio rerio.[3]
Así como en los organismos biológicos, los patrones de Turing aparecen en otros sistemas naturales, por ejemplo los patrones del viento formados en la arena. A pesar de que las ideas de Turing acerca de la morfogénesis y los patrones de Turing quedaron abandonadas por muchos años, ahora son inspiradores para investigaciones en biología matemática.[4]
Véase también
[editar]Referencias
[editar]- ↑ Turing, A. M. (1952). «The Chemical Basis of Morphogenesis». Philosophical Transactions of the Royal Society of London B 237 (641): 37-72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012.
- ↑ Harrison, L. G. (1993). Kinetic Theory of Living Pattern. Cambridge University Press.
- ↑ Roose, Tiina; Wertheim, Kenneth Y. (3 de enero de 2019). «Can VEGFC Form Turing Patterns in the Zebrafish Embryo?». Bulletin of Mathematical Biology (en inglés): 1-37. ISSN 1522-9602. PMID 30607882. doi:10.1007/s11538-018-00560-2.
- ↑ Woolley, T. E., Baker, R. E. Maini, P. K., Chapter 34, Turing's theory of morphogenesis. In Copeland, B. Jack; Bowen, Jonathan P.; Wilson, Robin; Sprevak, Mark (2017). The Turing Guide. Oxford University Press. ISBN 978-0198747826.
Bibliografía
[editar]- Kondo, Shigeru; Miura, Takashi (24 de septiembre de 2010). «Reaction-Diffusion Model as a Framework for Understanding Biological Pattern Formation». Science 329 (5999). pp. 1616-1620. doi:10.1126/science.1179047.
- Keim, Brandon (22 de febrero de 2011). «Alan Turing's Patterns in Nature and Beyond». Wired.
- Ball, Philip (31 de mayo de 2012). «Turing Patterns». Chemistry World.
- Ouellette, Jennifer (27 de marzo de 2013). «When Math Meets Nature: Turing Patterns and Form Constants». Scientific American.
- Campagna, R.; Cuomo, S.; Giannino, F.; Severino, G.; Toraldo, G. (6 de diciembre de 2017). «A semi-automatic numerical algorithm for Turing patterns formation in a reaction-diffusion model». IEEE Access 6: 4720-4724. doi:10.1109/ACCESS.2017.2780324.
- «New theory deepens understanding of Turing patterns in biology». Phys.org. European Molecular Biology Laboratory. 20 de junio de 2018.
- Iber, Bagnar. «Turing Pattern». Computational Biology (CoBI). Switzerland: ETH Zurich. Consultado el 16 de agosto de 2018.
Enlaces externos
[editar]- Esta obra contiene una traducción total derivada de «Turing Patterns » de Wikipedia en inglés, concretamente de esta versión, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.








